SURFACE AREA OF PRISMS AND CYLINDERS

Finding the Surface Area of a Prism

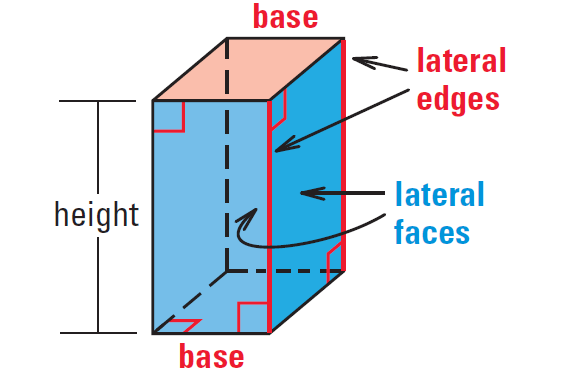
A prism is a polyhedron with two congruent faces, called bases, that lie in parallel planes. The other faces, called lateral faces, are parallelograms formed by connecting the corresponding vertices of the bases. The segments connecting these vertices are lateral edges.

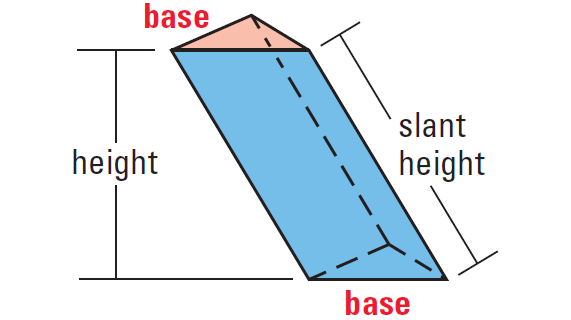
The altitude or height of a prism is the perpendicular distance between its bases. In a right prism, each lateral edge is perpendicular to both bases. Prisms that have lateral edges that are not perpendicular to the bases are oblique prisms. The length of the oblique lateral edges is the slant height of the prism.

Right Rectangular Prism :

Oblique Rectangular Prism :

Prisms are classified by the shapes of their bases. For example, the figures above show one rectangular prism and one triangular prism. The surface area of a polyhedron is the sum of the areas of its faces. The lateral area of a polyhedron is the sum of the areas of its lateral faces.

Imagine that you cut some edges of a right hexagonal prism and unfolded it. 

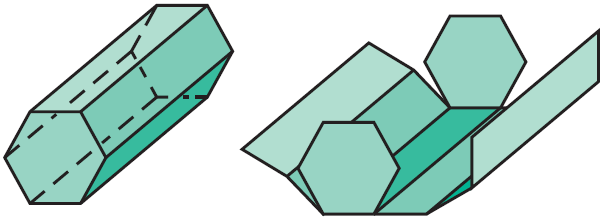
The two-dimensional representation of all of the faces is called a net. 

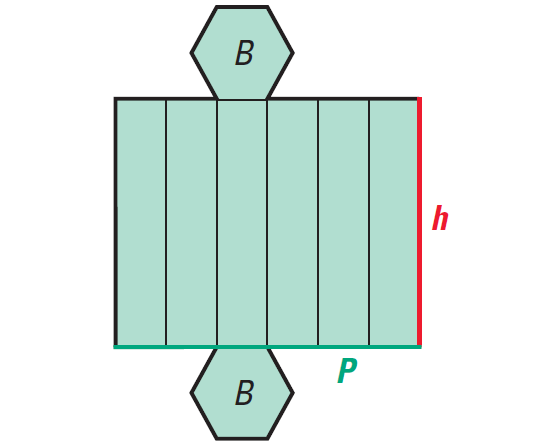
In the net of the prism, notice that the lateral area (the sum of the areas of the lateral faces) is equal to the perimeter of the base multiplied by the height. 

Surface Area of a Right Prism

Theorem :

The surface area S of a right prism can be found using the formula

S  =  2B + Ph

where B is the area of a base, P is the perimeter of a base, and h is the height.

Finding the Surface Area of a Cylinder

A cylinder is a solid with congruent circular bases that lie in parallel planes. The altitude, or height, of a cylinder is the perpendicular distance between its bases. The radius of the base is also called the radius of the cylinder. A cylinder is called a right cylinder, if the segment joining the centers of the bases is perpendicular to the bases.

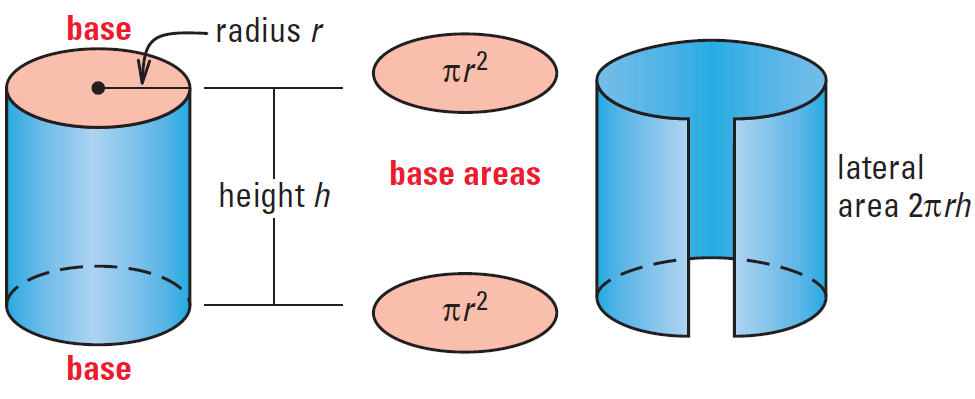
The lateral surface area is the area of its curved surface. The lateral area is equal to the product of the circumference and the height, which is 2πrh.

The entire surface area of a cylinder is equal to the sum of the lateral area and the areas of the two bases.

Surface Area of a Right Cylinder

Theorem :

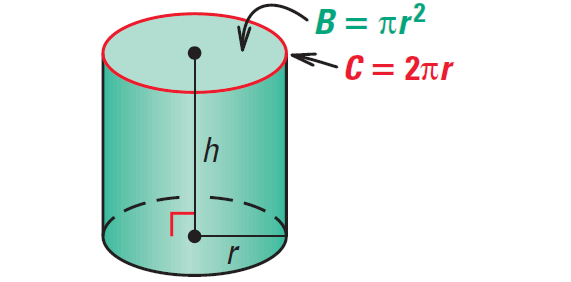
The surface area S of a right cylinder is

S  =  2B + Ch

S  =  2πr² + 2πrh

where B is the area of a base, C is the circumference of a base, r is the radius of a base, and h is the height.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.