SURFACE AREA OF COMBINED SHAPES

Find the surface area :

Example 1 :

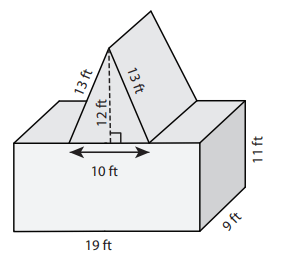
Solution :

In the given picture, we have a cuboid and a triangular prism.

Surface area of cuboid  =  2(lw + wh + hl)

l  =  19 ft, w  =  9 ft and h  =  11 ft

=  2(19x9 + 9x11 + 11x19)

=  2(171 + 99 + 209)

=  2(479)

=  958 square feet

Surface area of triangular prism  =  2(area of front and back face) + 2(area of side faces)

=  2(1/2) ⋅ 12 ⋅ 10 + 2(13⋅9)

=  120 + 234

=  354 square feet

=  958+354

=  1312

Now at the top, we have to ignore the base area of triangular prism. 

=  1312 - (10 x 9)

=  1312 - 90

=  1222 square feet

So, the required surface area of the picture given above is 1222 square feet.

Example 2 :

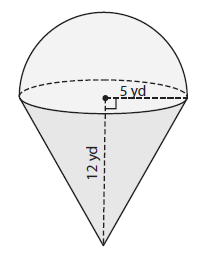
Solution :

Surface area of the shape  =  Curved surface area of cone + Curved surface area of hemisphere 

=  π rl + 2πr²

Slant height  =  √r²+h²

l = √5² + 12²

l = √(25 + 144)

l = 13

= π r(l+2r)

=  3.14 ⋅ 5(13+2(5))

=  3.14 ⋅ 5(23)

=  361.1 square yard

Example 3 :

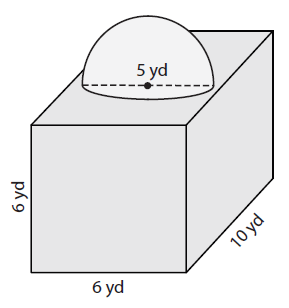
Solution :

Surface area of the given picture  =  Total surface area of cuboid - Curved surface area of base of hemisphere + curved surface area of hemisphere

=  2(lw + wh + hl) - πr² + 2πr²

=  2(lw + wh + hl) + πr² 

=  2 (36 + 60 + 60) + 3.14(2.5)²

=  2 (36 + 60 + 60) + 3.14(2.5)²

=  312 + 19.625

=  331.63 square yards.

Example 4 :

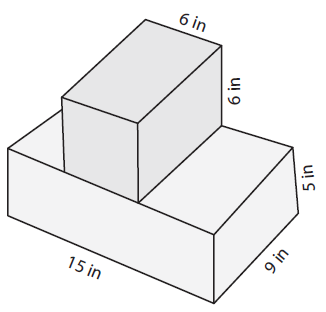
Solution :

Required area  =  Total surface area of rectangular prism at the top - Base area of top rectangular prism + area rectangular prism at the top (5 sides)

=  2(135+45+75) - 54 + (54+54+54+36+36)

=  2(255) - 54 + 234

=  510 - 54 + 234

=  690 square inches

Example 5 :

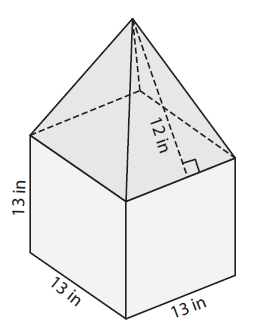
Solution :

Required area  =  Area of 5 sides of cube + Area of triangular prism with square base 

=  5 (13 ⋅ 13)  + 4 (1/2 ⋅ 13 ⋅ 12)

=  5 (169) + 2(156)

=  845 + 312

=  1157 square inches.

Example 6 :

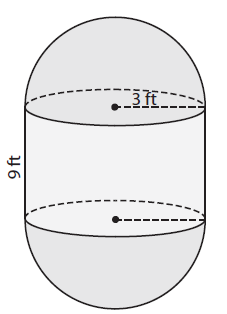
Solution :

Required area  =  Curved surface area of cylinder + surface area of 2 hemispheres

=  2π rh + 2 (2πr²)

=  2πr(h + 2r)

=  2 (3.14) 3 (9 + 6)

=  18.84 (15)

=  282.6 square feet

Example 7 :

Yanna celebrated her fifth birthday. She ate at her favorite restaurant. She ordered a soda pop. The soda pop came in a cup shaped like a cylinder with a cone top. The cylinder part of the cup was 6 inches tall and the height of the top was 2 inches. The radius of the cup was 2 inches. What was the surface area of the cup?

Solution :

height of cylinder = 6 inches

Height of cone = 2 inches

radius = 2 inches

Surface area of cup = surface area of cylinder + surface area of cone

= 2π rh + π rl

l = √r² + h²

l = √2² + 2²

l = √(4+4)

l = 2√2

= π[2rh + rl]

= 3.14[2 x 2 x 6 + 2 x 2.828]

= 3.14[24 + 5.656]

= 3.14[29.656]

= 93.119 square inches

Example 8 :

A circus tent is cylindrical up to a height of 4.2 m and conical above it. The common diameter of the base of cylindrical and conical parts is 6 m. If the total height of the tent from the ground is 8.2 m, find the cost of canvas needed to make the tent at the rate of $16 per m².

Solution :

Height of cylinder = 4.2 m

Diameter = 6 m, radius = 3 m

Total height of the tent = 8.2 m

height of cylinder + height of cone = 8.2

4.2 + height of cone = 8.2

height of cone = 8.2 - 4.2

= 4 m

Surface area of the tent = surface area of cylinder + surface area of cone

= 2π rh + π rl

l = √r² + h²

l = √3² + 4²

= √(9 + 16)

= √25

l = 5 m

= π r[2h + l]

= 3.14 x 3[2(4.2) + 5]

= 9.42[8.4 + 5]

= 9.42(13.4)

= 126.228 m²

Cost per square meter = 16

Required cost = 126.228 x 16

= $2019.648

Example 9 :

Volumes of two spheres are in the ratio 64 : 27. The ratio of their surface areas is

(a) 3:4     (b) 4:3     (c) 9:16     (d) 16:9

Solution :

Volume of two spheres = 64 : 27

Let r₁ and r₂ be radii of two spheres respectively.

(4/3)π r₁³ : (4/3)π r₂³ = 64 : 27

 r₁³ : r₂³  = 64 : 27

 r₁ : r₂  = 4 : 3

 r₁ / r₂  = 4 / 3

 r₁  = 4r₂/3

Surface area of sphere = 4π r₁² : 4π r₂²

= r₁² : r₂²

= (4r₂/3)² : r₂²

= (16r₂/9) : r₂²

= 16 : 9

Example 10 :

Two identical cubes each of volume 64 cm³ are joined together end to end. What is the surface area of the resulting cuboid?

(a) 512 cm²     (b) 192 cm²      (c) 160 cm²     (d) 128 cm²

Solution :

Volume of one cube = 64 cm³

Let a be the side length of cube.

a³ = 64

a = 4 cm

Length of cuboid = 4 + 4 ==> 8 cm

Width = 4 cm and height = 4 cm

Surface area of cuboid = 2(lw + wh + hl)

= 2(8 x 4 + 4 x 4 + 4 x 8)

= 2(32 + 16 + 32)

= 2(80)

= 160 cm²

So, option c is correct.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.