SUM OF THE ANGLE MEASURES IN A TRIANGLE

There is a special relationship between the measures of the interior angles of a triangle.

That is,

sum of the Three Angles in Any Triangle  =  180°

In the next part, we are going to justify this relationship.

Sum of the Angle Measures in a Triangle is 180° - Justify

Step 1 :

Draw a triangle and cut it out. Label the angles A, B, and C.

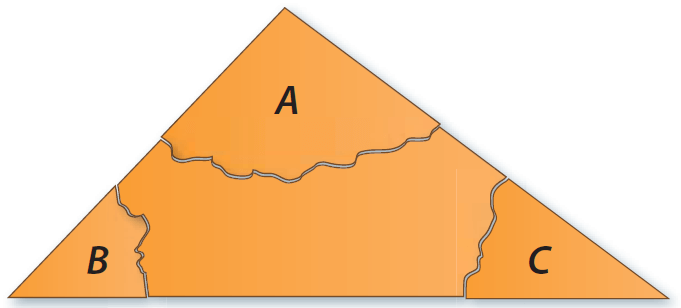
Step 2 :

Tear off each “corner” of the triangle. Each corner includes the vertex of one angle of the triangle.

Step 3 :

Arrange the vertices of the triangle around a point so that none of your corners overlap and there are no gaps between them.

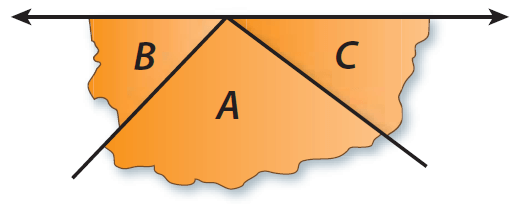
Step 4 :

What do you notice about how the angles fit together around a point?

The angles form a straight angle.

Step 5 :

What do you notice about how the angles fit together around a point?

180°

Step 6 :

Describe the relationship among the measures of the angles of triangle ABC?

The sum of the angle measures is 180°.

Step 7 :

What does the triangle sum theorem state?

The triangle sum theorem states that for triangle ABC,

m∠A + m∠B + m∠C = 180°

Reflect

1.  Can a triangle have two right angles ? Explain.

No

The sum of the measures of two right angles is 180°. That means the measure of the third angle would be

180° - 180° = 0°

which is impossible.

2. Describe the relationship between the two acute angles in a right triangle. Explain your reasoning.

No

They are complementary.

The sum of their measures must be

180° - (measure of the right angle) = 180° - 90° = 90°

Solved Problems

Problem 1 :

Can 30°, 60° and 90° be the angles of a triangle? 

Solution :

Let us add all the three given angles and check whether the sum is equal to 180°.

 30° +  60° + 90° = 180°

Since the sum of the angles is equal 180°, the given three angles can be the angles of a triangle.

Problem 2 :

Can 35°, 55° and 95° be the angles of a triangle?

Solution :

Let us add all the three given angles and check whether the sum is equal to 180°.

 35° +  55° + 95° = 185°

Because the sum of the angles is not equal 180°, the given three angles can not be the angles of a triangle.

Problem 3 :

In a triangle, if the second angle is 5° greater than the first angle and the third angle is 5° greater than second angle, find the three angles of the triangle.

Solution :

Let x be the first angle.

The second angle = x + 5.

The third angle = x + 5 + 5 = x + 10.

Sum of the three angles of a triangle = 180°

x + (x + 5) + (x + 10) = 180°

3x + 15 = 180

3x = 165

x = 55

The first angle = 55°.

The second angle = 55 + 5 = 60°.

The third angle = 60 + 5 = 65°.

So, the three angles of a triangle are 55°, 60° and 65°.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.