SUM OF INTERIOR ANGLES OF A POLYGON

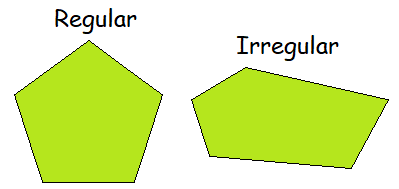
Regular and Irregular Polygons

Regular Polygon :

A regular polygon has sides of equal length, and all its interior and exterior angles are of same measure.

Irregular Polygon :

An irregular polygon can have sides of any length and angles of any measure.

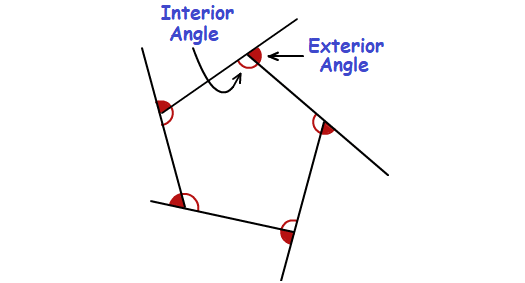
Interior and Exterior Angles of a Polygon

Interior Angle :

An interior angle of a polygon is an angle inside the polygon at one of its vertices.

Exterior Angle :

An exterior angle of a polygon is an angle outside the polygon formed by one of its sides and the extension of an adjacent side.

Example 1 :

Find the value of 'x in the diagram given below. 

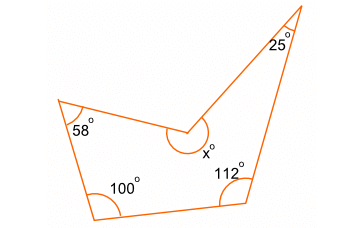
Solution :

The above diagram is an irregular polygon of 5 sides. 

Formula to find the sum of interior angles of a n-sided polygon is 

=  (n - 2) ⋅ 180°

By using the formula,  sum of the interior angles of the above polygon is 

=  (5 - 2) ⋅ 180°

=  3 ⋅ 180°

=  540° ------(1)

By using the angles, sum of the interior angles of the above polygon is  

=  58° + 100° + 112° + 25° + x°

=  295° + x° ------(2)

From (1) and (2), we get

295° + x°  =  540°

295 + x  =  540

Subtract 295 from both sides. 

x  =  245

Hence, the value of "x" is 245.

Example 2 :

Find the value of 'x' in the diagram given below. 

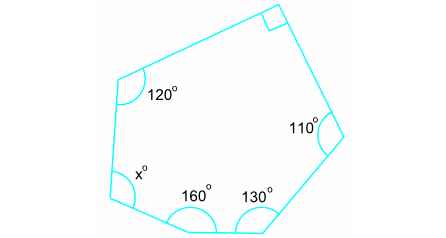
Solution :

The above diagram is an irregular polygon of 6 sides (Hexagon) with one of the interior angles as right angle. 

Formula to find the sum of interior angles of a n-sided polygon is 

=  (n - 2) ⋅ 180°

By using the formula,  sum of the interior angles of the above polygon is 

=  (6 - 2) ⋅ 180°

=  4 ⋅ 180°

=  720° ------(1)

By using the angles, sum of the interior angles of the above polygon is  

=  120° + 90° + 110° + 130° + 160 + x°

=  610° + x° ------(2)

From (1) and (2), we get

610° + x°  =  720°

610 + x  =  720

Subtract 610 from both sides. 

x  =  110

Hence, the value of "x" is 110.

Example 3 :

Find the measure of each interior angle of the regular polygon given below. 

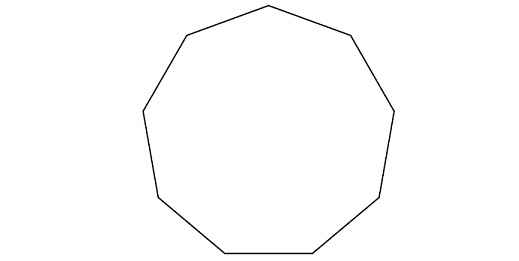
Solution :

Let us count the number of sides of the polygon given above. 

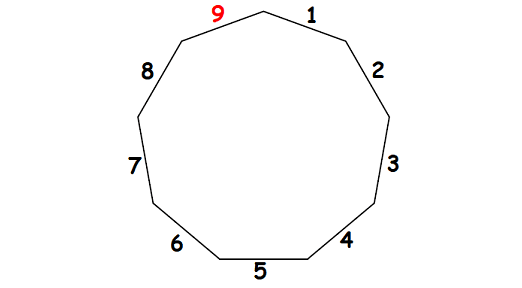
So, the above regular polygon has 9 sides. 

Formula to find the sum of interior angles of a n-sided polygon is 

=  (n - 2) ⋅ 180°

By using the formula,  sum of the interior angles of the above polygon is 

=  (9 - 2) ⋅ 180°

=  7 ⋅ 180°

=  1260°

Formula to find the measure of each interior angle of a n-sided regular polygon is   

=  Sum of interior angles / n

Then, we have

=  1260° / 9

=  140°

Hence, the measure of each interior angle of the given regular polygon is 140°.  

Example 4 :

What is the measure of each interior angle of a regular decagon ?

Solution :

Decagon is a 10-sided polygon.

Formula to find the sum of interior angles of a n-sided polygon is 

=  (n - 2) ⋅ 180°

By using the formula,  sum of the interior angles of the given decagon (10-sided polygon) is 

=  (10 - 2) ⋅ 180°

=  8 ⋅ 180°

=  1440°

Formula to find the measure of each interior angle of a n-sided regular polygon is   

=  Sum of interior angles / n

Then, we have

=  1440° / 10

=  144°

Hence, the measure of each interior angle of the given regular decagon is 144°.  

Example 5 :

Each exterior angle of a regular polygon measures 30°. How many sides does the polygon have ?

Solution :

Formula to find the number of sides of a regular polygon (when the measure of each exterior angle is known) : 

=  360 / Measure of each exterior angle 

Then, we have

=  360 / 30

=  12

Hence, the given polygon has 12 sides. 

Example 6 :

Each interior angle of a regular polygon measures 160°. How many sides does the polygon have ?

Solution :

In any polygon, the sum of an interior angle and its corresponding exterior angle is 180°.

That is,

Interior angle + Exterior Angle  =  180°

160° + Exterior Angle  =  180°

Exterior angle  =  20°

So, the measure of each exterior angle is 20°.

Formula to find the number of sides of a regular polygon (when the measure of each exterior angle is known) : 

=  360 / Measure of each exterior angle 

Then, we have

=  360 / 20

=  18

Hence, the given polygon has 18 sides. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.