STRAIGHT LINE PROBLEMS WITH SOLUTIONS

Problem 1 :

A photocopy store charges $1.50 per copy for the first 10 copies and $1.00 per copy after the 10th copy. Let x be the number of copies, and let y be the total cost of photocopying (i) Draw graph of the cost as x goes from 0 to 50 copies (ii) Find the cost of making 40 copies.

Solution :

(i) :

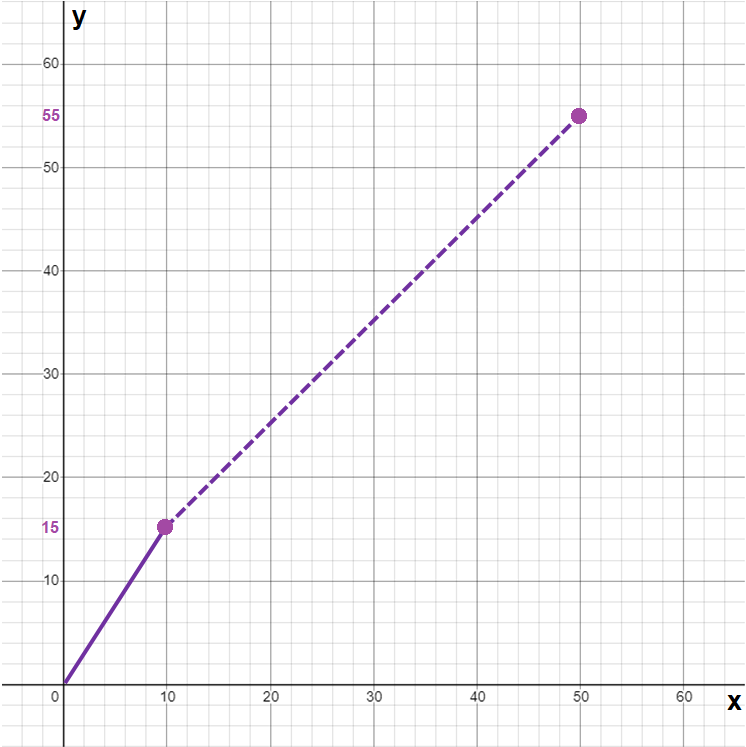
(ii) :

x stands for number of copies and y stands for total cost.

y  =  1.5x  for  0 ≤ x ≤ 10

After 10th copy, cost per copy is $1.00. 

Let us construct a function for the number of copies which is greater than 10.

y  =  1.5(10) + 1(x - 10)

y  =  15 + x - 10

y  =  5 + x  for x > 10

Substitute 40 for x. 

y  =  x + 5

=  40 + 5

=  45

The cost of making 40 copies is $45.

Problem 2 :

Find at least two equations of the straight lines in the family of the lines y = 5x + b, for which b and the x-coordinate of the point of intersection of the lines with 3x - 4y = 6 are integers.

Solution :

Find the point of intersection of the above lines using substitution.

y  =  5x + b

3x - 4y  =  6

Substitute (5x + b) for y in 3x - 4y = 6.

3x - 4(5x + b)  =  6

3x - 20x - 4b  =  6

-17x - 4b  =  6

-17x  =  6 + 4b

x  =  -(6 + 4b)/17

Since x is an integer,  (6 + 4b) has to be a multiple of 17.

6 + 4b  =  ±17, ±34,...............

6 + 4b = 17 ----> b = 11/4 (not an integer)

6 + 4b = -17 ----> b = -23/4 (not an integer)

6 + 4b = 34 ----> b = 7 (integer)

6 + 4b = -34 ----> b = -10 (integer)

The required equations are

y  =  5x + 7

y  =  5x - 10

Problem 3 :

Find all the equations of the straight lines in the family of the lines y = mx - 3, for which m and the x-coordinate of the point of intersection of the lines with x - y = 6 are integers.

Solution :

Find the point of intersection of the above lines using substitution.

y = mx − 3

x - y = 6

Substitute (mx - 3) for y in x - y = 6. 

x - (mx - 3)  =  6

x - mx + 3  =  6

x - mx  =  3

x(1 - m)  =  3

x  =  3/(1 - m)

Find the possible integer values of m such that the value of x is also an integer.

m = -2 ----> x = 3/3 = 1

m = 0 ----> x = 3/1 = 3

m = 2 ----> x = 3/(-1) = -3

m = 4 ----> x = 3/(-3) = -1

The possible integer values of m are -2, 0, 2 and 4.

The required equations are

y  =  -2x - 3

y  =  -3

y  =  2x - 3

y  =  4x - 3

Problem 4 :

The line y = (1/2) x – 5 passes through the points W and X. The point W has co-ordinates (8, a). The point X has co-ordinates (b, 8).

(a) Find a.

(b) Find b.

Solution :

y = (1/2) x – 5

) The value of a is -1

b) Value of b is 26.

Problem 5 :

If line through the points  (-2, 6) and (4, 8) is perpendicular to the line through the points (8, 12) and (x, 24). Find the value of x.

Solution :

The line joining the points  (-2, 6) and (4, 8) and the line joining the points (8, 12) and (x, 24) are perpendicular.

If two lines are perpendicular, then the product of their slopes = -1.

Slope of the line joining the points (-2, 6) and (4, 8) :

m = (y₂ - y₁)/(x₂ - x₁)

m = (8 - 6) / (4 + 2)

= 2/6

m₁ = 1/3

Slope of the line joining the points (8, 12) and (x, 24) :

m = (y₂ - y₁)/(x₂ - x₁)

m = (24 - 12) / (x - 8)

= 12/(x - 8)

m₂ = 12/(x - 8)

m₁  ⋅ m₂ = 1/3 ⋅ [12/(x - 8)]

-1 = 4/(x - 8)

-1(x - 8) = 4

-x + 8 = 4

-x = 4 - 8

-x = -4

x = 4

So, the value of x is 4.

Problem 6 :

The line L has equation y = 3x + 13. Circle the line(s) that are parallel to L.

a)  y = 2x + 13     b)  y = 3x + 1

c)  y = 4x + 12      d)  y = -3x + 13

Solution :

y = 3x + 13

When two lines are parallel, then their slopes will be equal.

y = 3x + 13

Comparing with y = mx + b, we get m = 3

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.