STEM AND LEAF PLOTS

For numbers with two digits, 

the first digit forms part of the stem and

the second digit forms part of the leaf.

For example, for the data value 17, 1 is recorded on the stem, and the 7 is a leaf value.

Make the stem and leaf plots for the given data :

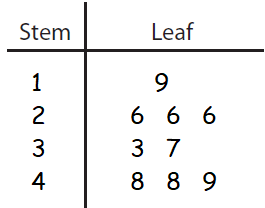
Example 1 :

26, 37, 48, 33, 49, 26, 19, 26, 48

Solution :

Arrange the given data set in ascending order.

19, 26, 26, 26, 33, 37, 48, 48, 49

Example 2 :

67, 42, 58, 41, 54, 65, 65, 54, 69, 53

Solution :

Writing the given data values in ascending order, we get

41, 42, 53, 54, 54, 58, 65, 65, 67, 69

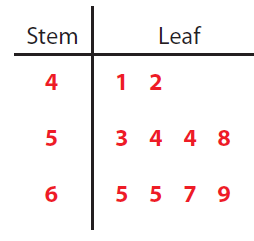
Example 3 :

For the ordered stem-and-leaf plot given, find:

(a)  the minimum value

(b)  the maximum value

Solution :

The first entry can be considered as minimum value

stem  =  0, leaf  =  1

Minimum value  =  1

The last entry can be considered as maximum value.

stem  =  4, leaf  =  3

Minimum value  =  43.

Example 4 :

A test score out of 60 marks is recorded for a group of 45 students :

34 37 44 51 53 39 33 58 40 42

43 43 47 37 35  41 43 48 50 55

44 44 52 54 59 39 31 29 44 57

45 34 29 27 18 49 41 42 37 42

43 43 45 34 51

a) Construct a stem-and-leaf plot for this data using 0, 1, 2, 3, 4, and 5 as the stems.

b) What advantage does a stem-and-leaf plot have over a frequency table?

c) What is the

i) highest     ii) lowest mark scored for the test?

d) If an ‘A’ is awarded to students who scored 50 or more for the test, what percentage of students scored an ‘A’?

e)  What percentage of students scored less than half marks for the test?

f)  Describe the distribution of the data.

Solution :

(a) 

(b)  The stem-and-leaf plot shows all the actual data values.

(c)  i)  Highest mark is 59

ii)  Lowest mark  =  18

(d) Total number of marks  =  45

Number of students who scores 50 or more than 50  =  10

Percentage  =  (10/45) x 100%

=  22.2 %

Percentage of students who scored more than 50 percentage of marks is 22.2%

(e)  Number of students who scored less than half mark

=  4

Percentage  =  (4/45) x 100%

=  8.88%

e) Negatively skewed with no outliers

Example 5 :

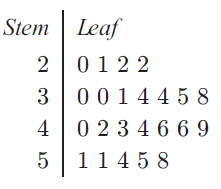
For the data set given, find:

a) the minimum value

b) the maximum value

c) the median

d)  the range

Solution :

(a)  The first entry is minimum value

stem  =  2, leaf  =  0

Minimum value  =  20

(b)  The last entry is maximum value

stem  =  5, leaf  =  8

Maximum value  =  58

c)  Total number of values  =  23

23 is odd, so median  =  (23+1)/2

=  24/2

Median  =  12^th value

So, median is 40.

(d)  Range  =  maximum value - minimum value

=  58-20

=  38

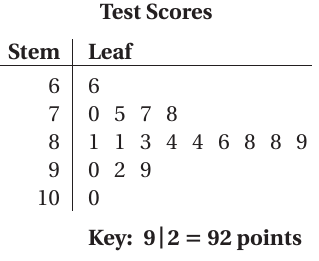
Example 6 :

The stem-and-leaf plot shows student test scores.

(a) How many students scored less than 80 points?

(b) How many students scored at least 90 points?

(c) How are the data distributed?

Solution :

a) There are five scores less than 80 points:

66, 70, 75, 77, and 78

Five students scored less than 80 points.

b) There are four scores of at least 90 points:

90, 92, 99, and 100

Four students scored at least 90 points.

c) There are few low test scores and few high test scores. So, most of the scores are in the middle.

Example 7 :

Which statement is not true?

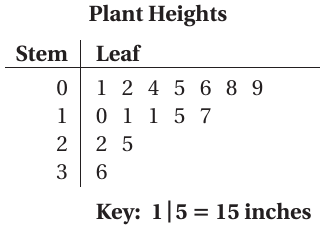
A)   Most of the plants are less than 20 inches tall.

B)   The median plant height is 11 inches.

C)   The range of the plant heights is 35 inches.

D)   The plant height that occurs most often is 11 inches.

Solution :

There are 15 plant heights. So, the median is the eighth data value, 10 inches. The correct answer is option B.

Example 8 :

a) How many data values are in the set?

b) What is the least value? greatest value?

c) What is the median? range?

d)  Is the value 32 in the set? Explain

Solution :

a)  The values are

4, 6, 8, 10, 23, 24, 30, 36, 36, 37, 42

Total number of values are 11.

b)  The least value = 4

greatest value = 42

c)  Median :

Total number of values are 11, then median

= (11 + 1)/2^th term 

= 12/2^th term

= 6^th term

So, the median = 24

d) 32 is not one of the value.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.