STANDARD FORM TO VERTEX FORM BY COMPLETING THE SQUARE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
In this section, you will learn how to convert the standard form of a quadratic function to vertex form by completing the square.
The standard form a quadratic function is
y = ax2 + bx + c
The vertex form a quadratic function is
y = a(x - h)2 + k
Here, the vertex is (h, k).
Following are the steps to convert the standard form of a quadratic function to vertex form.
Step 1 :
In the given quadratic function y = ax2 + bx + c, factor "a" from the first two terms of the quadratic expression on the right side.
Then,
y = ax2 + bx + c
y = a(x2 + bx/a) + c
Note :
If the coefficient of x2 is 1 (a = 1), the above process is not required.
Step 2 :
In the result of step 1, write the "x" term as a multiple of 2.
Examples :
6x should be written as 2(3)(x).
5x should be written as 2(x)(5/2).
Then, the result of this step will be :
y = a[x2 + 2(x)(b/a)] + c
Step 3 :
Now add and subtract (b/a)2 inside the parentheses to complete the square on the left side.
Then,
y = a[x2 + 2(x)(b/a) + (b/a)2 - (b/a)2] + c
Step 4 :
In the result of step 3, if we use the algebraic identity
(a + b)2 = a2 + 2ab + b2
inside the parentheses, we get
y = a[(x + b/a)2 - (b/a)2] + c
Simplify.
y = a[(x + b/a)2 - b2/a2] + c
y = a(x + b/a)2 - b2/a + c
y = a(x + b/a)2 - b2/a + ac/a
y = a(x + b/a)2 + (ac - b2)/a
The above quadratic is in the form of
y = a(x - h)2 + k
Here, the vertex is (h, k).
Examples 1-2 :Convert the equation of the parabola from standard form to vertex form and sketch the parabola.
Example 1 :
y = x2 - 4x + 3
Solution :
Step 1 :
In the quadratic function given, the coefficient of x2 is 1. So, we can skip step 1.
Step 2 :
In the quadratic function y = x2 - 4x + 3, write the "x" term as a multiple of 2.
Then,
y = x2 - 2(x)(2) + 3
Step 3 :
Now add and subtract 22 on the right side to complete the square.
Then,
y = x2 - 2(x)(2) + 22 - 22 + 3
y = x2 - 2(x)(2) + 22 - 4 + 3
y = x2 - 2(x)(2) + 22 - 1
Step 4 :
In the result of step 3, if we use the algebraic identity
(a - b)2 = a2 - 2ab + b2
on the right side, we get
y = (x - 2)2 - 1
The quadratic function above is in vertex form.
Comparing
y = (x - 2)2 - 1
and
y = a(x - h)2 + k,
the vertex is
(h, k) = (2, -1)
and
a = 1
Graph of the Parabola :
The vertex of the parabola is (2, -1). Because the sign of a is positive the parabola opens upward.
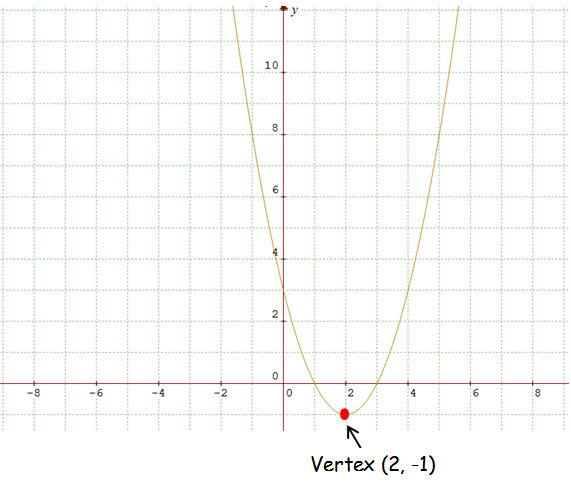
Example 2 :
y = 2x2 - 8x + 9
Solution :
Step 1 :
In the quadratic function given, the coefficient of x2 is 2. So, factor "2" from the first two terms of the quadratic expression on the right side.
y = 2(x2 - 4x) + 9
Step 2 :
In the quadratic function y = 2(x2 - 4x) + 9, write the "x" term as a multiple of 2.
Then,
y = 2[x2 - 2(x)(2)] + 9
Step 3 :
Now add and subtract 22 inside the parentheses to complete the square.
Then,
y = 2[x2 - 2(x)(2)+ 22 - 22] + 9
y = 2[x2 - 2(x)(2)+ 22 - 4] + 9
Step 4 :
In the result of step 3, if we use the algebraic identity
(a - b)2 = a2 - 2ab + b2
inside the parentheses, we get
y = 2[(x - 2)2 - 4] + 9
y = 2(x - 2)2 - 8 + 9
y = 2(x - 2)2 + 1
The quadratic function above is in vertex form.
Comparing
y = 2(x - 2)2 + 1
and
y = a(x - h)2 + k,
the vertex is
(h, k) = (2, 1)
and
a = 2
Graph of the Parabola :
The vertex of the parabola is (2, 1). Because the sign of a is positive the parabola opens upward.
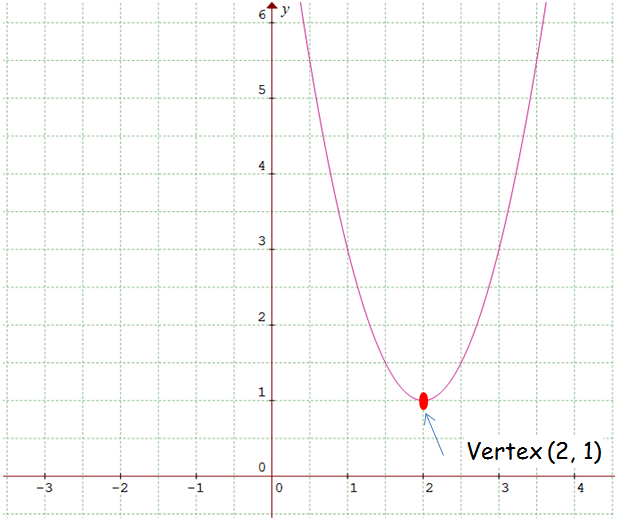
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 40)
Dec 25, 25 08:30 AM
10 Hard SAT Math Questions (Part - 40) -
10 Hard SAT Math Questions (Part - 41)
Dec 24, 25 07:58 PM
10 Hard SAT Math Questions (Part - 41) -
ASTC Formula in Trigonometry
Dec 23, 25 11:34 PM
ASTC Formula in Trigonometry - Concepts - Examples and Solved Problems


