STANDARD FORM OF A QUADRATIC FUNCTION

The standard form of a quadratic function is 

y  =  ax² + bx + c

where a, b and c are real numbers, and a  ≠  0.

Using Vertex Form to Derive Standard Form

Write the vertex form of a quadratic function. 

y  =  a(x - h)² + k

Square the binomial. 

y  =  a(x² - 2xh + h²) + k

y  =  ax² - 2ahx + ah² + k

The equation y  =  ax² - 2axh + ah² + k is a quadratic function in standard form with 

a  =  a

b  =  - 2ah

c  =  ah² + k

The vertex of a quadratic function is (h, k), so to determine the x-coordinate of the vertex, solve b = -2ah for h.

b  =  -2ah

Divide each side by -2a.

- b / 2a  =  h

Because h is the x-coordinate of the vertex, we can use this value to find the y-value, k, of the vertex.  

Example : 

Find the vertex of the quadratic function :

f(x)  =  x² - 8x + 12

Solution : 

Step 1 : 

Identify the coefficients a, b and c. 

Comparing  

ax² + bx + c  and  x² - 8x + 12,  

we get

a  =  1, b  =  -8  and  c  =  12

Step 2 : 

Solve for h, the x-coordinate of the vertex. 

h  =  - b / 2a

Substitute. 

h  =  - (-8) / 2(1)

h  =  8 / 2

h  =  4

Step 3 : 

Substitute the value of h into the equation for x to find k, the y-coordinate of the vertex.

f(4)  =  4² - 8(4) + 12

f(4)  =  16 - 32 + 12

f(4)  =  - 4

So, the vertex of the given quadratic function is 

(h, k)  =  (4, -4)

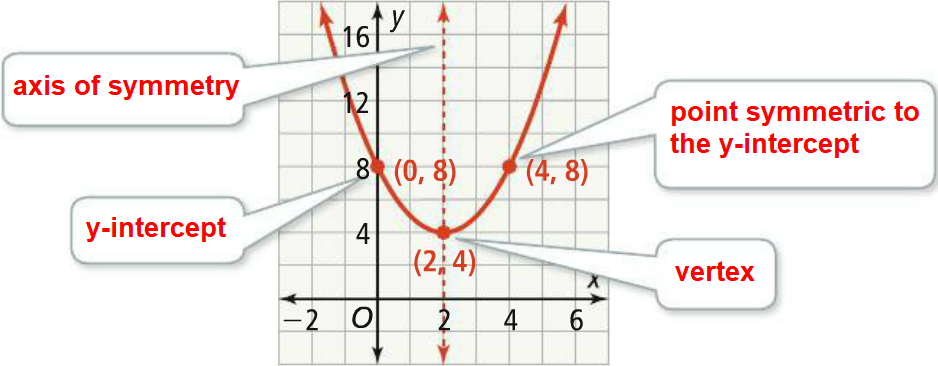
Graphing a Quadratic Function in Standard Form

Example : 

Graph the quadratic function :

f(x)  =  x² - 4x + 8

Solution : 

Step 1 : 

Identify the coefficients a, b and c. 

Comparing  

ax² + bx + c  and  x² - 4x + 8,  

we get

a  =  1, b  =  -4  and  c  =  8

Step 2 : 

Find the vertex of the quadratic function.

The x-coordinate of the vertex can be determined by

h  =  - b / 2a

Substitute. 

h  =  - (-4) / 2(1)

h  =  4 / 2

h  =  2

Substitute the value of h for x into the equation to find the y-coordinate of the vertex, k :

f(2)  =  2² - 4(2) + 8

f(2)  =  4 - 8 + 8

f(2)  =  4

So, the vertex is

(h, k)  =  (2, 4)

Step 3 : 

Find the axis of symmetry of the quadratic function.

Axis of symmetry of a quadratic function can be determined by the x-coordinate of the vertex. 

In the vertex (2, 4), the x-coordinate is 2. 

So, the axis of symmetry is 

x  =  2

Step 4 : 

Find the y-intercept of the quadratic function. 

To find the y-intercept, put x = 0. 

f(0)  =  0² - 4(0) + 8

f(0)  =  8

Step 5 : 

Find a point symmetric to the y-intercept across the axis of symmetry. 

Because (0, 8) is point on the parabola 2 units to the left of the axis of symmetry, x  =  2, (4, 8) will be a point on the parabola 2 units to the right of the axis of symmetry. 

Step 6 : 

Sketch the graph. 

Once we have three points associated with the quadratic function, we can sketch the parabola based on our knowledge of its general shape. 

Interpreting the Graph of a Quadratic Function

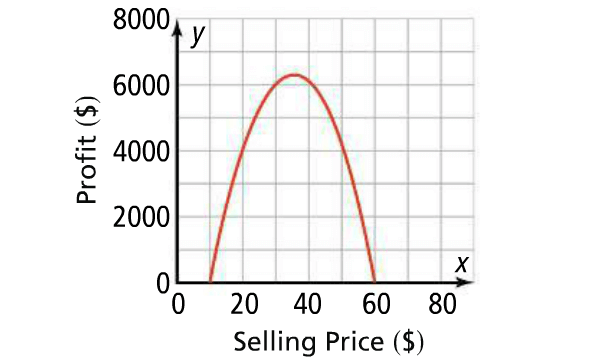
Example :

The graph of a quadratic function

f(x)  =  - 10x² + 700x - 6000

shows the profit, a company earns for selling items at different prices. Find the maximum profit that the company can expect to earn. 

Solution :

The x-axis shows the selling price and the y-axis shows the profit. 

The maximum y-value of the profit function occurs at the vertex of its parabola. Find the vertex of the parabola. 

Use the function to find the x-coordinate and y-coordinate of the vertex. 

Find the x-coordinate of the vertex. 

h  =  - b / 2a

Substitute.

h  =  - 700 / 2(-10)

h  =  - 700 / (-20)

h  =  35

Find the y-coordinate of the vertex. 

y  =  - 10x² + 700x - 6000

Substitute  x  =  35.

y  =  - 10(35)² + 700(35) - 6000

Simplify.

y  =  - 12250 + 24500 - 6000

y  =  6250

So, the vertex is 

(h, k)  =  (35, 6250)

So, the selling price of $35 per item gives the maximum profit of $6,250.

Writing the Equation of a Parabola Given Three Points

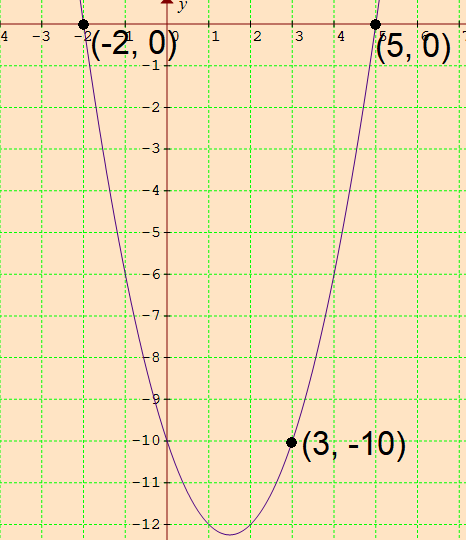
Example : 

Find the equation of a parabola that passes through the points : 

(-2, 0), (3, -10) and (5, 0)

Solution :

Step 1 : 

Write the three equations by substituting the given x and y-values into the standard form of a parabola equation,

y  =  ax² + bx + c

Substitute (-2, 0).

0  =  a(-2)² + b(-2) + c

0  =  4a - 2b + c

Substitute (3, -10).

-10  =  a(3)² + b(3) + c

-10  =  9a + 3b + c

Substitute (5, 0).

0  =  a(5)² + b(5) + c

0  =  25a + 5b + c

Step 2 : 

Solve the system :

0  =  4a - 2b + c

-10  =  9a + 3b + c

0  =  25a + 5b + c

Solving the above system using elimination method,  we will get

a  =  1,  b  =  - 3  and  c  =  - 10

Step 3 :

Substitute 1 for a, -3 for b, and -10 for c in the standard form of quadratic equation.

Hence, the equation of a parabola is 

y  =  x² - 3x - 10

Step 4 : 

Confirm that the graph of the equation passes through the given three points.  

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.