STANDARD EQUATION OF A PARABOLA

Given : 

∙ Fixed point (F)

∙ Fixed line or directrix (l)

∙ Eccentricity (e = 1)

∙ Moving point P(x, y)

Construction : 

∙ Plot the fixed point F and draw the fixed line ‘l’.

∙ Drop a perpendicular (FZ) from F to l.

∙ Draw a perpendicular bisector to FZ and treat it as y-axis.

∙ Let V(0, 0) be the origin.

∙ Drop a perpendicular (PM) from P to l.

∙ The known points are F(a, 0), Z(-a, 0) and M is (-a, y). 

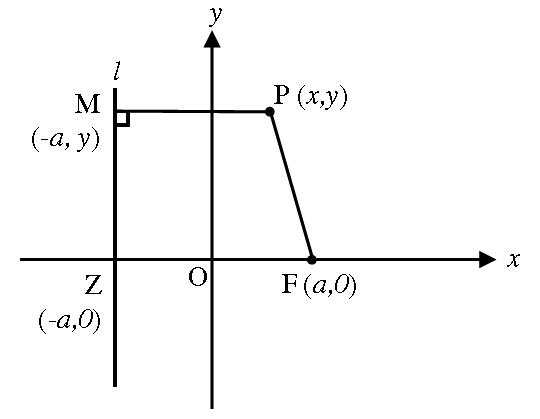
By the definition of a conic,

FP/PM  =  e  =  1

FP/PM  =  1

FP  =  PM

Square both sides. 

FP²  =  PM²

(x - a)² + (y - 0)²  =  (x + a)² + (y - y)²

x² - 2ax + a² + y²  =  x² + 2ax + a²

Subtract x² and a² from each side. 

- 2ax + y²  =  2ax

Add 2ax to each side. 

y²  =  4ax

This is the standard equation of the parabola with vertex at origin.

Graph of y²  =  4ax : 

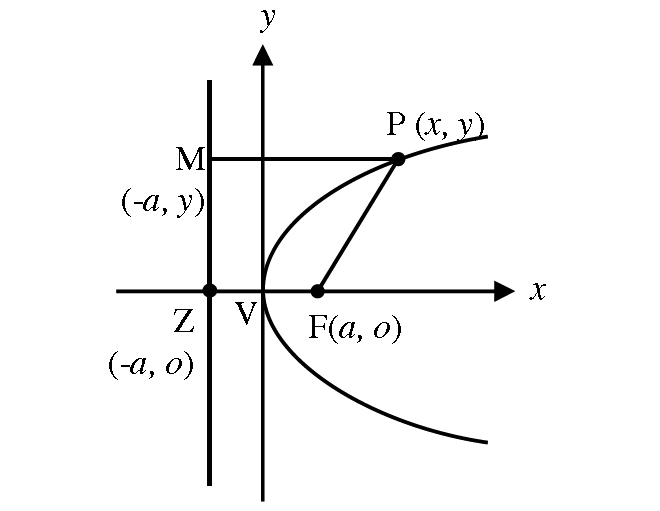
If the vertex is other then origin, say (h, k), then

(y - k)²  =  4a(x - h)

Other Standard Parabolas

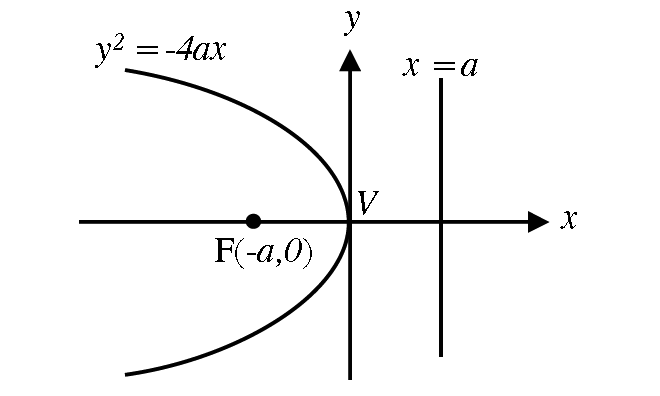
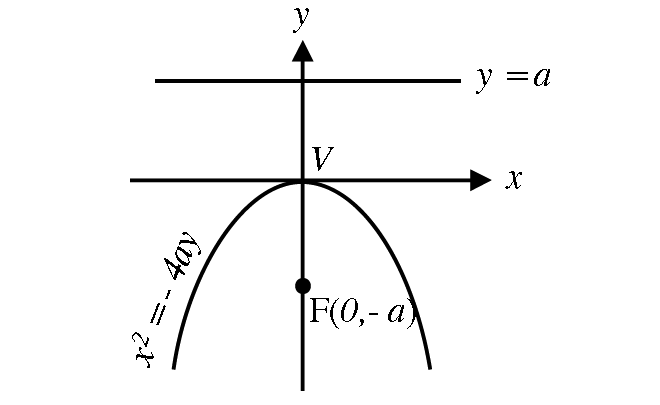
1. Open leftward : y²  =  -4ax [a > 0]

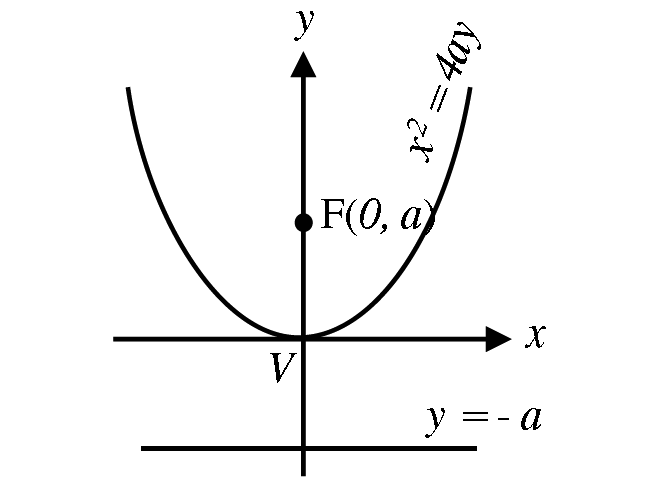
2. Open upward : x²  =  4ay [a > 0]

3. Open downward : x²  =  -4ay [a > 0]

Solved Problems

Use the information provided to write the standard equation of each parabola.

Problem 1 : 

Vertex at origin, Focus (0, 1)

Solution : 

Plot the vertex (0, 0) and focus (0, 1) on the xy-plane. 

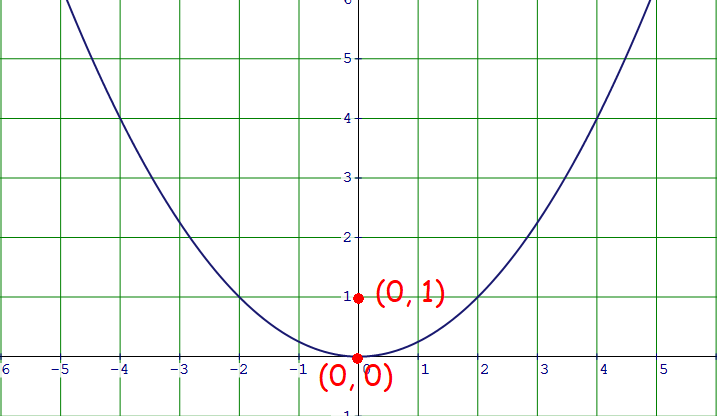
The parabola is open up with vertex at origin. 

Standard equation of a parabola that opens up with vertex at origin :

x²  =  4ay

Distance between the vertex and focus is 1 unit. 

That is, a = 1. 

x²  =  4(1)y

x²  =  4y

Problem 2 : 

Vertex at origin, Focus (2, 0)

Solution : 

Plot the vertex (0, 0) and focus (2, 0) on the xy-plane.

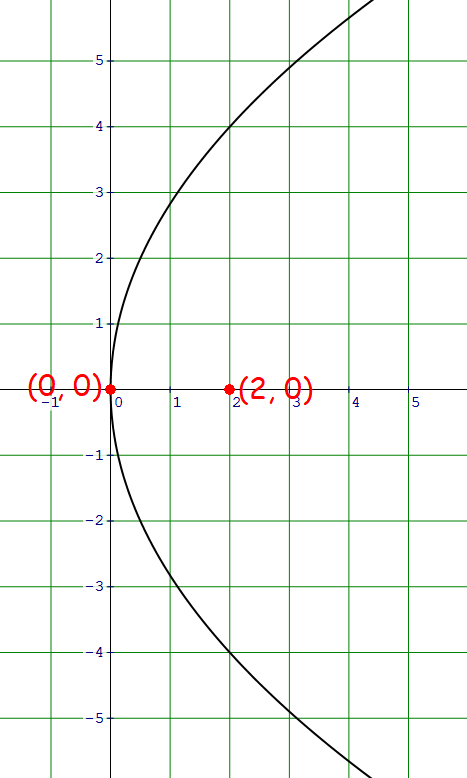
The parabola is open to the right with vertex at origin. 

Standard equation of a parabola that opens right with vertex at origin : 

y²  =  4ax

Distance between the vertex and focus is 2 units. 

That is, a = 2. 

y²  =  4(2)x

y²  =  8x

Problem 3 : 

Vertex at (1, 2), Focus (1, -1)

Solution : 

Plot the vertex (1, 2) and focus (1, -1) on the xy-plane.

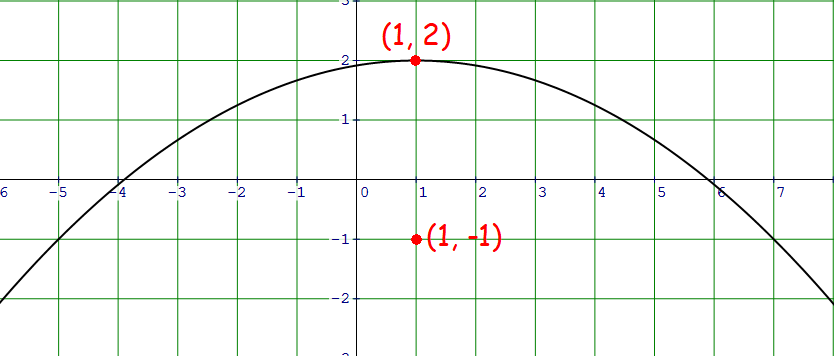
The parabola is open down with vertex at (1, 2). 

Standard equation of a parabola that opens down with vertex at (h, k) : 

(x - k)²  =  -4a(y - h)

Vertex (h, k) = (1, 2).

(x - 1)²  =  -4a(y - 2)

Distance between the vertex and focus is 3 units. 

That is, a = 3. 

(x - 1)²  =  -4(3)(y - 2)

(x - 1)²  =  -12(y - 2)

Problem 4 : 

Vertex at (2, -1), Focus (-1, -1)

Solution : 

Plot the vertex (2, -1) and focus (-1, -1) on the xy-plane.

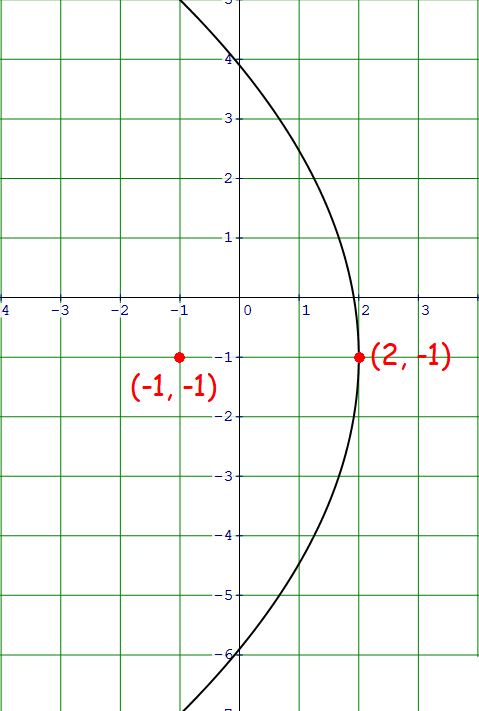
The parabola is open to the left with vertex at (2, -1).

Standard equation of a parabola that opens left with vertex at (h, k) : 

(y - k)²  =  -4a(x - h)

Vertex (h, k) = (2, -1).

(y + 1)²  =  -4a(x - 2)

Distance between the vertex and focus is 3 units. 

That is, a = 3. 

(y + 1)²  =  -4(3)(x - 2)

(y + 1)²  =  -12(x - 2)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.