SQUARE ROOTS OF FRACTIONS

Previously we have seen

3²  =  9

indicates that

√9  =  3

Similarly,

(4/5)²  =  16/25

indicates that

√(16/25)  =  4/5

From this, we observe 

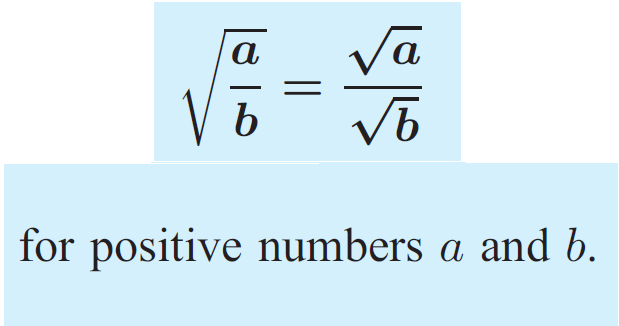
Example 1 :

Find √(4/9)

Solution :

√(4/9)  =  √4/√9

=  √(2⋅2)/√(3⋅3)

=  2/3

Example 2 :

Find √(2  1/4)

Solution :

√(2  1/4)  =  √(9/4)

√(9/4)  =  √9/√4

=  √(3⋅3)/√(2⋅2)

=  3/2

Example 3 :

Find √(25/9)

Solution :

√(25/9)  =  √25/√9

=  √(5⋅5)/√(3⋅3)

=  5/3

Example 4 :

Find √(36/169)

Solution :

√(36/169)  =  √36/√169

=  √(6⋅6)/√(13⋅1)

=  6/13

Example 5 :

Find √(160/5)

Solution :

√(160/5) 

If it is possible, we can simplify and then find the square root.

=  √32

=  √(2⋅2⋅2⋅2⋅2)

=  2⋅2√2

√(160/5)  =  4√2

Example 6 :

Find √(18/32)

Solution :

=  √(18/32) 

If it is possible, we can simplify and then find the square root.

=  √9/16 

=  √9/√16 

=  √(3⋅3)/√(4⋅4)

√(18/32)  =  3/4

Example 7 :

Find √(50/8)

Solution :

=  √(50/8) 

If it is possible, we can simplify and then find the square root.

=  √25/4 

=  √25/√4 

=  √(5⋅5)/√(2⋅2)

√(50/8)  =  5/2

Example 8 :

Find √(0.25/0.36)

Solution :

=  √(0.25/0.36) 

First change numerator and denominator as integer, and then take the square roots separately.

√(0.25/0.36)  =  √(25/100)/(36/100) 

=  √(25/36)

=  √25/√36

=  √(5⋅5)/√(6⋅6)

=  5/6

Example 9 :

Find √(0.81/0.4)

Solution :

=  √(0.81/0.4) 

First change numerator and denominator as integer, and then take the square roots separately.

√(0.81/0.4)  =  √(81/100)/(4/10) 

=  √(81/100)⋅(10/4) 

=  √(81/40)

=  √81/√40

=  √(9⋅9)/√(2⋅2⋅2⋅5)

=  9/2√10

Example 10 :

Find √(a³/b⁵)

Solution :

=  √(a³/b⁵)

=  √a³/√b⁵

=  √(a⋅a⋅a)/√(b⋅b⋅b⋅b⋅b)

=  a√a/(b⋅b)√b

=  a√a/b²√b

Example 11 :

Given that √4096 = 64, the value of √4096 + √40.96 is

a)  74     b)  60.4     c)  64.4      d)  70.4

Solution :

Given that √4096 = 64

To get the value of 40.96, let us make 40.96 as integer. To do that, by considering the number of digits after the decimal, it is 2. So, we have to multiply both numerator and denominator by 100.

 √40.96 = √(4096/100)

= √(64⋅64/10⋅10)

= 64/10

= 6.4

√4096 + √40.96 = 64 + 6.4

= 70.4

Example 12 :

Find the square root of 0.09

Solution :

To find the square root of 0.09, first we have to make the decimal as fraction.

To do that, we have to look at the number of digits after the decimal. Since we have two digits after the decimal, we have to multiply both numerator and denominator by 100.

√0.09 = √0.09 x (100/100)

= √(9/100)

= √(3⋅3/10⋅10)

= 3/10

Since we have one zero at the denominator, we have to move the decimal that we find at last to one digit forward.

So, the answer is 0.3

Example 13 :

Find the square root of 0.0064

Solution :

To find the square root of 0.0064, first we have to make the decimal as fraction.

To do that, we have to look at the number of digits after the decimal. Since we have four digits after the decimal, we have to multiply both numerator and denominator by 100000.

√0.0064 = √0.0064 x (10000/10000)

= √(64/10000)

= √(8⋅8/100⋅100)

= 8/100

Since we have two zeroes at the denominator, we have to move the decimal that we find at last to two digits forward.

So, the answer is 0.08.

Example 14 :

Find the value of x in

x/√162 = √128/x

Solution :

x/√162 = √128/x

Doing cross multiplication, we get

x(x) = √128 √162

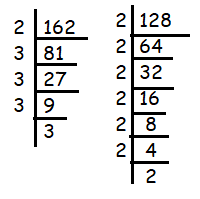
x² = √(2⋅3⋅3⋅3⋅3) √(2⋅2⋅2⋅2⋅2⋅2⋅2)

Using the property of square root,

 √a  √b =  √(a ⋅ b)

x² = √(2⋅3⋅3⋅3⋅3) (2⋅2⋅2⋅2⋅2⋅2⋅2)

For every two same values which are multiplied inside the radical, we have to take away one value out of the radical.

x² = (2⋅2⋅2⋅2⋅3⋅3)

x = √(2⋅2⋅2⋅2⋅3⋅3)

Taking one value for every two same values.

x = 12

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.