SQUARE ROOT OF FRACTIONS AND DECIMALS WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
1. Find the square root of 4/9.
2. Find the square root of 169/289.
3. Find the square root of 2.56.
4. Find the square root of 51.84.
5. Find the square root of 0.2916.

1. Answer :
√(4/9) = √4 / √9
When we decompose 4 and 9 into prime factors, we get
4 = 22
9 = 32
Then, we have
√(4/9) = √22 / √32
√(4/9) = 2/3
So, the square root of 4/9 is 2/3.
2. Answer :
√(169) = √169 / √289
When we decompose 169 and 289 into prime factors, we get
169 = 132
289 = 172
Then, we have
√(169/289) = √132 / √172
√(169/289) = 13/17
So, the square root of 169/289 is 13/17.
3. Answer :
Convert the decimal number 2.56 into a fraction.
Because there are two digits after the decimal point, multiply and divide 2.56 by 100 to get rid of the decimal point.
2.56 = (2.56 ⋅ 100) / 100
2.56 = 256 / 100
Take square root on each side.
√2.56 = √(256/100)
Take square separately for numerator and denominator.
√2.56 = √256 / √100 -----(1)
To find the square root of 256 and 100, decompose 256 and 100 into prime factors using synthetic division as shown below.
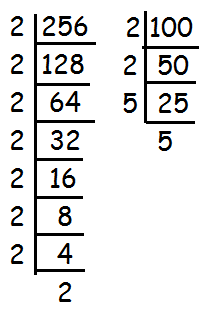
From the above synthetic division, we have
256 = 28
100 = 22 ⋅ 52
Then, we have
(1)-----> √2.56 = √28 / √(22 ⋅ 52)
√2.56 = 24 / (2 ⋅ 5)
√2.56 = 16 / 10
√2.56 = 1.6
So, the square root of 2.56 is 1.6.
4. Answer :
Convert the decimal number 51.84 into a fraction.
Because there are two digits after the decimal point, multiply and divide 51.84 by 100 to get rid of the decimal point.
51.84 = (51.84 ⋅ 100) / 100
51.84 = 5184 / 100
Take square root on each side.
√51.84 = √(5184/100)
Take square separately for numerator and denominator.
√51.84 = √5184 / √100 -----(1)
To find the square root of 5184 and 100, decompose 5184 and 100 into prime factors using synthetic division as shown below.
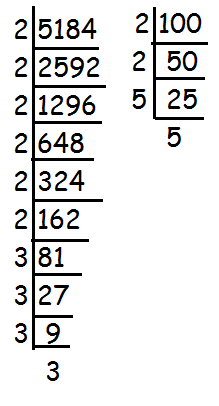
From the above synthetic division, we have
5184 = 26 ⋅ 34
100 = 22 ⋅ 52
Then, we have
(1)-----> √51.84 = √(26 ⋅ 34) / √(22 ⋅ 52)
√51.84 = (23 ⋅ 32) / (2 ⋅ 5)
√51.84 = (8 ⋅ 9) / 10
√51.84 = 72/10
√51.84 = 7.2
So, the square root of 51.84 is 7.2.
5. Answer :
Convert the decimal number 0.2916 into a fraction.
Because there are four digits after the decimal point, multiply and divide 0.2916 by 10000 to get rid of the decimal point.
0.2916 = (0.2916 ⋅ 10000) / 10000
0.2916 = 2916 / 10000
Take square root on each side.
√0.2916 = √(2916/10000)
Take square separately for numerator and denominator.
√0.2916 = √2916 / √10000 -----(1)
To find the square root of 2916 and 10000, decompose 2916 and 10000 into prime factors using synthetic division as shown below.
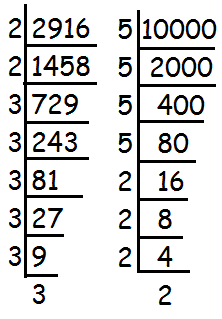
From the above synthetic division, we have
2916 = 22 ⋅ 36
10000 = 54 ⋅ 24
Then, we have
(1)-----> √0.2916 = √(22 ⋅ 36) / √(54 ⋅ 24)
√0.2916 = √(22 ⋅ 36) / √(54 ⋅ 24)
√0.2916 = (2 ⋅ 33) / (52 ⋅ 22)
√0.2916 = (2 ⋅ 27) / (25 ⋅ 4)
√0.2916 = 54/100
√0.2916 = 0.54
So, the square root of 0.2916 is 0.54.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 45)
Jan 19, 26 06:14 AM
10 Hard SAT Math Questions (Part - 45) -
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations
