SQUARE ROOT OF A NUMBER

You can find square root of any positive number and the result is defined. You can not find square root of a negative number. Because, square root of any negative number is imaginary or undefined.

In general, square root of a positive number is always positive. This is called principal square root.

For example, let us consider √4. In √4, there is no positive or negative sign in front of the square root. In front of any number, if there is no positive or negative sign, we always assume there is positive sign.

So, √4 = 2. This is called principal square root.

Principal square root of any positive number is always positive.

Here, you may have a question. Some people are taking positive or negative sign (±) infront of square root of a number. Why?

Conider the equation given below.

x² = 9 ----(1)

When x = 3, 

x² = 3²

x² = 9

If x = 3, we have x² = 9. So, (1) is true for x = 3.

Is (1) true only for x = 3 or for any other value of x?

What if x = -3?

x² = (-3)²

x² = (-3)(-3)

x² = 9

If x = -3 also, we have x² = 9. So, (1) is true for x = -3.

So, the equation x² = 9 is true for both x = 3 and x = -3.

Let x be a variable and k be a positive real number.

Then the equation in the form x² = k will have two solutions.

x = ±√k

When we solve an equation in the form x² = k, we will be taking square root on both sides to get rid of the square we have for x on the left side. When we take square root for the positive number k on right side, we have to consider both positive and negative sign.

How to Find Square Root of a Number

There are two methods to find square root of a number.

1. Prime factorization

2. Long Division Method

In each case, evaluate the square root :

Example 1 :

√9

Solution :

√9 = √(3 ⋅ 3)

= 3

Example 2 :

√25

Solution :

√25 = √(5 ⋅ 5)

= 5

Example 3 :

√8

Solution :

√8 = √(2 ⋅ 2 ⋅ 2)

= 2√2

Example 4 :

√27

Solution :

√27 = √(3 ⋅ 3 ⋅ 3)

= 3√3

Example 5 :

√72

Solution :

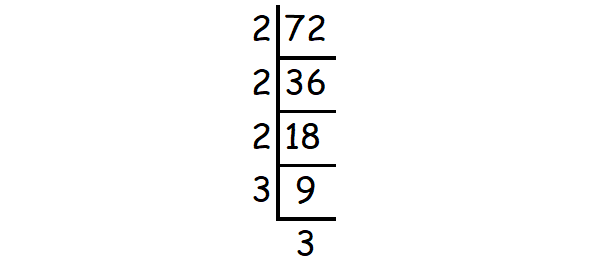
√72 = √(2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 3)

= (2 ⋅ 3)√(2 ⋅ 3)

= 6√6

Example 6 :

√0.36

Solution :

√0.36

Inside the square root, we have a decimal number. To get rid of the decimal point, we can write 0.36 as a fraction. In 0.36, since there are two digits after the decimal point, we can write it as a fraction with denominator 100.

√0.36 = √³⁶⁄₁₀₀

= √(⁶⁄₁₀ ⋅ ⁶⁄₁₀) 

= ⁶⁄₁₀

= 0.6

Example 7 :

√1.69

Solution :

√1.69 = √¹⁶⁹⁄₁₀₀

= √(¹³⁄₁₀ ⋅ ¹³⁄₁₀) 

= ¹³⁄₁₀

= 1.3

Example 8 :

√0.04

Solution :

√0.04 = √⁴⁄₁₀₀

= √(²⁄₁₀ ⋅ ²⁄₁₀) 

= ²⁄₁₀

= 0.2

Square Root by Long Division Method

Example 9 :

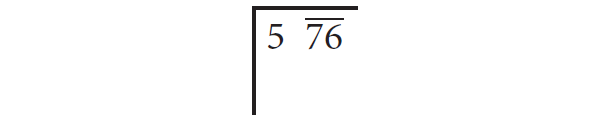
Find the square root of 576 by long division method.

Solution :

Step 1 :

Group the digits in pairs, starting with the digit in the unit’s place. Each pair and the remaining digit (if any) is called a period. Put a bar over every pair of digits starting from the right of the given number. If there are odd number of digits, the extreme left digit will be without a bar sign above it.

Step 2 :

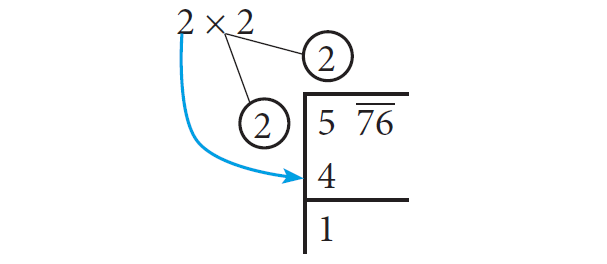
Th ink of the largest number whose square is equal to or just less than the fi rst period. Take this number as the divisor and also as the quotient. The left extreme number here is 5. Th e largest number whose square is less than or equal to 5 is 2. Th is is our divisor and the quotient.

Step 3 :

Bring 76 down and write it down to the right of the remainder 1. Now, the new dividend is 176.

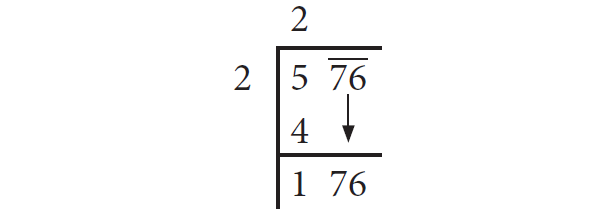
Step 4 :

To find the new divisor, multiply the earlier quotient (2) by 2 (always) and write it leaving a blank space next to it.

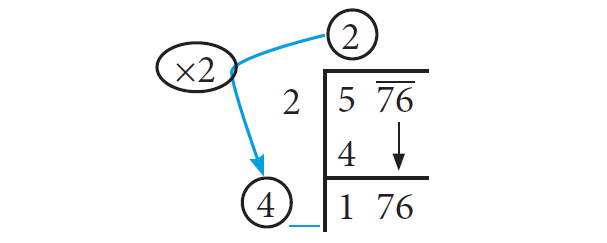
Step 5 :

The new divisor is 4 followed by a digit. We should choose
this digit next to 4 such that the new quotient multiplied by the new divisor will be less than or equal to 176.

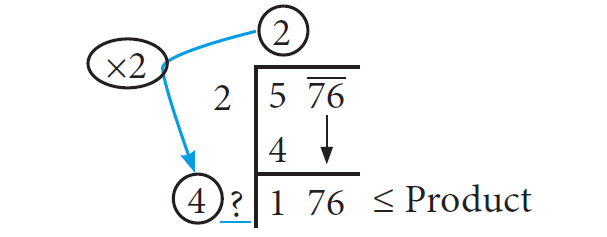
Step 6 :

Clearly, the required digit here has to be 4 or 6. (Why?) When we calculate, 46 x 6 = 276 whereas 44 x 4 = 176.  So, we put 4 in the blank space and write 44 x 4 = 176 below 176 and subtract to get the remainder 0 and the quotient at the top, that is 24 is the square root of 576.

Therefore,

√576 = 24

Solving Equations

In each case, solve for y :

Example 10 :

y² = 16

Solution :

y² = 16

To get rid of the square on the left side, take square root on both sides.

√y² = ±√16

y = ±√(4 ⋅ 4) 

y = ±4

y = -4  or  y = 4

Example 11 :

y² + 3 = 3

Solution :

y² + 3 = 3

Subtract 3 from both sides.

y² = 0

Take square root on both sides.

√y² = ±√0

y = 0

For zero, considering positive sign or negative sign will yield the same result. So, we don't have to consider positive or negative sign for zero.

Example 12 :

5y² = 180

Solution :

5y² = 180

Divide both sides by 5.

y² = 36

Take square root on both sides.

√y² = ±√36

y = ±√(6 ⋅ 6)

y = ±6

y = -6  or  y = 6

Example 13 :

36y² = 1

Solution :

36y² = 1

Divide both sides by 36.

y² = ¹⁄36

Take square root on both sides.

√y² = ±√¹⁄36

y = ±√(¹⁄6 ⋅ ¹⁄6)

v = ±¹⁄6

v = -¹⁄6  or  v = ¹⁄6

Example 14 :

y² - 2 = 6

Solution :

y² - 2 = 6

Add 2 to both sides.

y² = 8

Take square root on both sides.

√y² = ±√8

y = ±√(2 ⋅ 2 ⋅ 2)

y = ±2√2

y = -2√2  or  y = 2√2

Example 15 :

(5y² + 5)/2 = 25

Solution :

(5y² + 5)/2 = 25

Multiply both sides by 2.

5y² + 5 = 50

Subtract 5 from both sides.

5y² = 45

Divide both sides by 5.

y² = 9

Take square root on both sides.

√y² = ±√9

y = ±√(3 ⋅ 3)

y = ±9

y = -3  or  y = 3

Example 16 :

7 - 3y² = -236

Solution :

7 - 3y² = -236

Subtract 7 from both sides.

-3y² = -243

Divide both sides by -3.

y² = 81

Take square root on both sides.

√y² = ±√81

y = ±√(9 ⋅ 9)

y = ±9

y = -9  or  y = 9

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.