SQUARE AND CUBE ROOTS OF RATIONAL NUMBERS WORKSHEET

Problem 1 : 

Find the square root of 64.

Problem 2 : 

Find the square root of (1/4).

√(1/4)

Problem 3 : 

Find the cube root of (8/125). 

Problem 4 : 

Find the cube root of (1/64). 

Problem 5 : 

Find the square root of (36/81). 

Problem 6 : 

Find the square root (81/100). 

Problem 7 : 

Find the cube root of (125/216). 

Problem 8 : 

Find the cube root of (27/343). 

Problem 1 : Find the square root of 64. Solution : Step 1 : √64 Decompose the number inside the radical sign into prime factors.    =  √(2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2) Step 2 : Since the index is 2, we have to take one number out of radical sign for every two same numbers multiplied inside the radical sign.    =  2 ⋅ 2 ⋅ 2    =  8

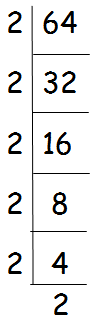Problem 2 :

Find the square root of (1/4). 

Solution : 

Step 1 :

√(1/4)

Distribute the square root to numerator and denominator.

=  √1 / √4

Step 2 :

Decompose 4 into its prime factors. 

=  1 / √(2 ⋅ 2)

Step 3 :

Since the index is 2, we have to take one number out of radical sign for every two same numbers multiplied inside the radical sign. 

  =  1/2

Problem 3 :

Find the cube root of (8/125). 

Solution : 

Step 1 :

³√(8/125)

Distribute the cube root to numerator and denominator.

=  ³√8 / ³√125

Step 2 :

Decompose the number inside the radical sign into prime factors. 

=  ³√(2 ⋅ 2 ⋅ 2) / ³√(5 ⋅ 5 ⋅ 5)

Step 3 :

Since the index is 3, we have to take one number out of radical sign for every three same numbers multiplied inside the radical sign. 

  =  2/5

Problem 4 :

Find the cube root of (1/64). 

Solution : 

Step 1 :

³√(1/64)

Distribute the cube root to numerator and denominator.

=  ³√1 / ³√64

Step 2 :

Decompose the number inside the radical sign into prime factors. 

=  ³√(1 ⋅ 1 ⋅ 1) / ³√(4 ⋅ 4 ⋅ 4)

Step 3 :

Since the index is 3, we have to take one number out of radical sign for every three same numbers multiplied inside the radical sign. 

=  1/4

Problem 5 :

Find the square root of (36/81). 

Solution :

Step 1 :

√(36/81)

Distribute the square root to numerator and denominator. 

=  √36 / √81

Step 2 :

Decompose the number inside the radical sign into prime factors. 

=  √(2 ⋅ 2 ⋅ 3 ⋅ 3) / √(3 ⋅ 3 ⋅ 3 ⋅ 3)

Step 3 :

Since the index is 2, we have to take one number out of radical sign for every two same numbers multiplied inside the radical sign. 

=  (2 ⋅ 3) / (3 ⋅ 3)

=  2/3

Problem 6 :

Find the square root (81/100). 

Solution : 

Step 1 :

√(81/100)

Distribute the square root to numerator and denominator. 

=  √(81/100)

=  √81 / √100

Step 2 :

Decompose the number inside the radical sign into prime factors. 

=  √(3 ⋅ 3 ⋅ 3 ⋅ 3) / √(10 ⋅ 10)

Step 3 :

Since the index is 2, we have to take one number out of radical sign for every two same numbers multiplied inside the radical sign. 

=  (2 ⋅ 3) / (3 ⋅ 3)

=  2/3

Problem 7 :

Find the cube root of (125/216). 

Solution :

Step 1 :

³√(125/216)

Distribute the cube root to numerator and denominator.

=  ³√125 / ³√216

Step 2 :

Decompose the numbers inside the radical sign into prime factors. 

=  ³√(5 ⋅ 5 ⋅ 5) / ³√(6 ⋅ 6 ⋅ 6)

Step 3 :

Since the index is 3, we have to take one number out of radical sign for every three same numbers multiplied inside the radical sign. 

=  5/6

Problem 8 :

Find the cube root of (27/343). 

Solution :

Step 1 :

³√(27/343)

Distribute the cube root to numerator and denominator. 

=  ³√27 / ³√343

Step 2 :

Decompose the number inside the radical sign into prime factors. 

=  ³√(3 ⋅ 3 ⋅ 3) / ³√(7 ⋅ 7 ⋅ 7)

Step 3 :

Since the index is 3, we have to take one number out of radical sign for every three same numbers multiplied inside the radical sign. 

=  3/7

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.