SPECIAL QUADRILATERALS AND THEIR PROPERTIES

A quadrilateral is a closed plane figure bounded by four line segments. For example, the figure ABCD shown below is a quadrilateral.

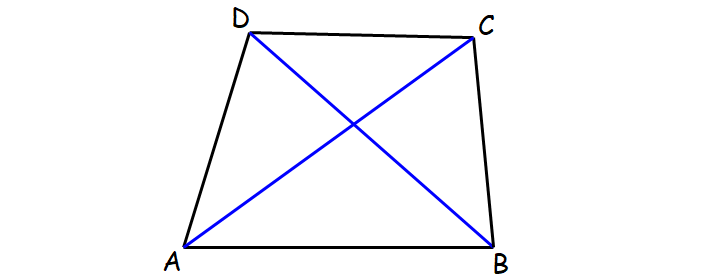
A line segment drawn from one vertex of a quadrilateral to the opposite vertex is called a diagonal of the quadrilateral.

For example, AC is a diagonal of quadrilateral ABCD, and so is BD.

There are six types of special quadrilaterals as shown in the diagram below.

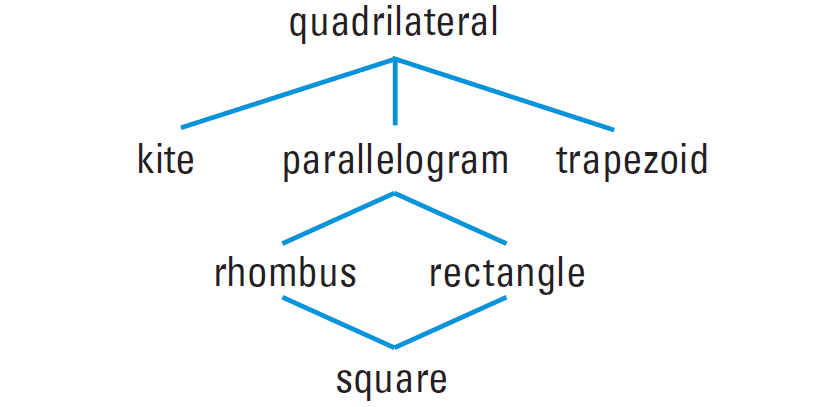
Special Quadrilaterals and Their Properties

Kite :

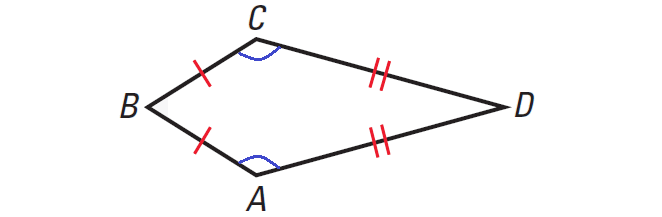
Properties of Kite :

Two pairs of consecutive congruent sides, but opposite sides are not congruent.

Exactly one pair of opposite angles are equal.

Diagonals intersect at right angles.

The longest diagonal bisects the shortest diagonal into two equal parts.

Parallelogram :

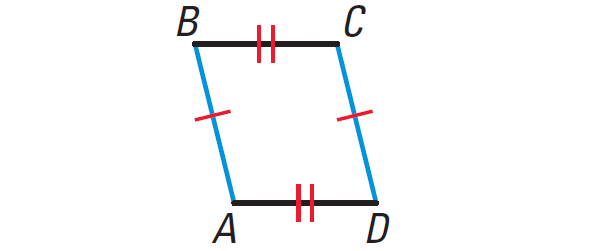
Properties of Parallelogram :

Opposite sides are parallel and equal.

Opposite angles are equal.

Diagonals bisect each other.

Trapezoid :

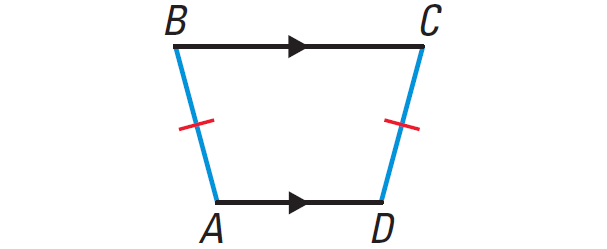
Properties of Trapezoid :

A trapezium has exactly one pair of opposite sides parallel.

A regular trapezium has non-parallel sides equal and its base angles are equal as shown in the diagram above.

Rhombus :

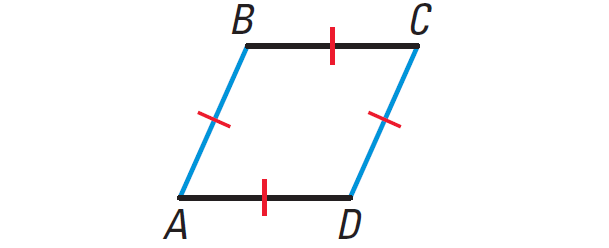
Properties of Rhombus :

All sides are equal and opposite sides are parallel.

Opposite angles are equal.

The diagonals bisect each other at right angles.

Rectangle :

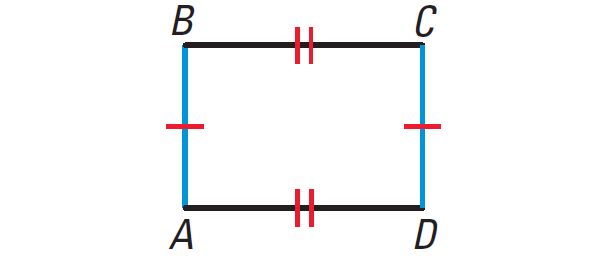
Properties of Rectangle :

Opposite sides are parallel and equal.

All angles are 90º.

The diagonals bisect each other.

Square :

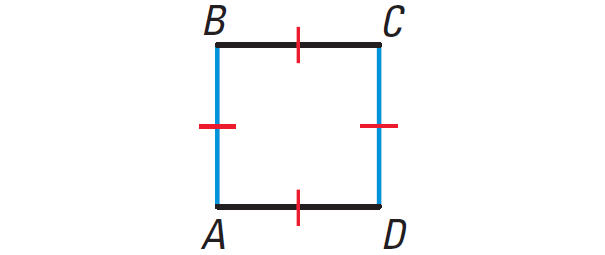
Properties of Square :

Opposite sides are parallel and all sides are equal.

All angles are 90º.

Diagonals bisect each other at right angles.

Solved Questions

Question 1 :

"A quadrilateral has at least one pair of opposite sides congruent"

What type of special quadrilateral can meet the above condition ?

Answer :

There are many possibilities.

Parallelogram :

Opposite sides are congruent.

Rhombus :

All sides are congruent.

Rectangle :

Opposite sides are congruent.

Square :

All sides are congruent.

Isosceles Trapezoid :

Legs are congruent.

Question 2 :

When we join the midpoints of the sides of any quadrilateral, what type of special quadrilateral formed ? Explain your answer.

Answer :

Let E, F, G and H be the midpoints of the sides of the quadrilateral ABCD shown below.

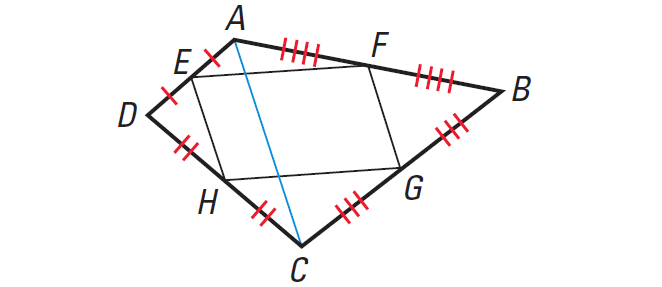
If we draw AC, the Midsegment Theorem for Triangles says

FG || AC and EH || AC ----> FG || EH

Similar reasoning shows that

EF || HG

So, by definition, EFGH is a parallelogram.

Hence, when the midpoints of the sides of any quadrilateral are joined, the type of special quadrilateral formed is parallelogram.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.