SPECIAL PRODUCTS OF BINOMIALS WORKSHEET

Problems 1-10 : Expand.

Problem 1 :

(y + 3)²

Problem 2 :

(2p + 3q)²

Problem 3 :

(5 + k²)²

Problem 4 :

(-x + 2)²

Problem 5 :

(1 + z³)²

Problem 6 :

(m - 5)²

Problem 7 :

(5k - 1)²

Problem 8 :

(4e - 5f)²

Problem 9 :

(4 - d²)²

Problem 10 :

(p² - q²)²

Problems 11-14 : Expand.

Problem 11 :

(m + n)(m - n)

Problem 12 :

(x + 3)(x - 3)

Problem 13 :

(c² + 2d)(c² - 2d)

Problem 14 :

(7 + y)(7 - y)

Problem 15 :

A square koi pond is surrounded by a gravel path. Write an expression that represents the area of the path. 

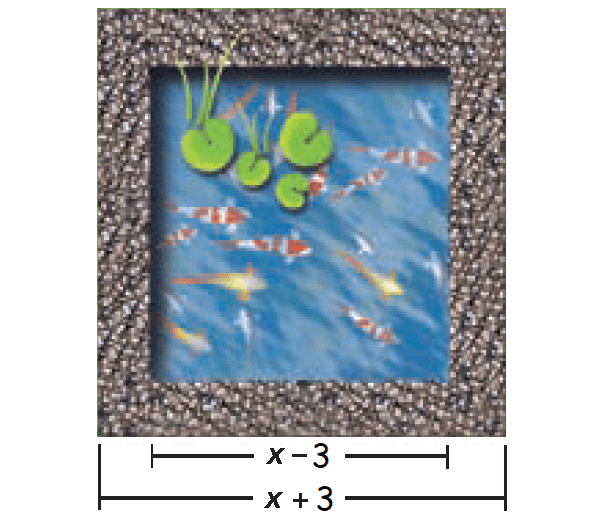
Answers

1. Answer :

Use the rule for (a + b)².

(a + b)² = a² + 2ab + b²

Identify a and b : a = y and b = 3.

(y + 3)² = y² + 2(y)(3) + 3²

= y² + 6y + 9

2. Answer :

Use the rule for (a + b)².

(a + b)² = a² + 2ab + b²

Identify a and b : a = 2p and b = 3q.

(2p + 3q)² = (2p)² + 2(2p)(3q) + (3q)²

= 4p² + 12pq + 9q²

3. Answer :

Use the rule for (a + b)².

(a + b)² = a² + 2ab + b²

Identify a and b : a = 5 and b = k².

(5 + k²)² = 5² + 2(5)(k²) + (k²)²

= 25 + 10k² + k⁴

4. Answer :

Use the rule for (a + b)².

(a + b)² = a² + 2ab + b²

Identify a and b : a = -x and b = 2.

(-x + 2)² = (-x)² + 2(-x)(2) + 2²

= x² - 4x + 4

5. Answer :

Use the rule for (a + b)².

(a + b)² = a² + 2ab + b²

Identify a and b : a = 1 and b = z³.

(1 + z³)² = 1² + 2(1)(z³) + (z³)²

= 1 + 2z³ + z⁶

6. Answer :

Use the rule for (a - b)².

(a - b)² = a² - 2ab + b²

Identify a and b : a = m and b = 5.

(m - 5)² = m² - 2(m)(5) + 5²

= m² - 10m + 25

7. Answer :

Use the rule for (a - b)².

(a - b)² = a² - 2ab + b²

Identify a and b : a = 5k and b = 1.

(5k - 1)² = (5k)² - 2(5k)(1) + 1²

= 25k² - 10k + 1

8. Answer :

Use the rule for (a - b)².

(a - b)² = a² - 2ab + b²

Identify a and b : a = 4e and b = 5f.

(4e - 5f)² = (4e)² - 2(4e)(5f) + (5f)²

= 16e² - 40ef + 25f²

9. Answer :

Use the rule for (a - b)².

(a - b)² = a² - 2ab + b²

Identify a and b : a = 4 and b = d².

(4 - d²)² = 4² + 2(4)(d²) + (d²)²

= 16 + 8d² + d⁴

10. Answer :

Use the rule for (a - b)².

(a - b)² = a² - 2ab + b²

Identify a and b : a = p² and b = q².

(p² - q²)² = (p²)² + 2(p²)(q²) + (q²)²

= p⁴ + 2p²q² + q⁴

11. Answer :

Use the rule for (a + b)(a - b).

(a + b)(a - b) = a² - b²

Identify a and b : a = m and b = n.

(m + n)(m - n) = m² - n²

12. Answer :

Use the rule for (a + b)(a - b).

(a + b)(a - b) = a² - b²

Identify a and b : a = x and b = 3.

(x + 3)(x - 3) = x² - 3²

= x² - 9

13. Answer :

Use the rule for (a + b)(a - b).

(a + b)(a - b) = a² - b²

Identify a and b : a = c² and b = 2d.

(c² + 2d)(c² - 2d) = (c²)² - (2d)²

= c⁴ - 4d²

14. Answer :

Use the rule for (a + b)(a - b).

(a + b)(a - b) = a² - b²

Identify a and b : a = 7 and b = y.

(7 + y)(7 - y) = 7² - y²

= 49 - y²

15. Answer :

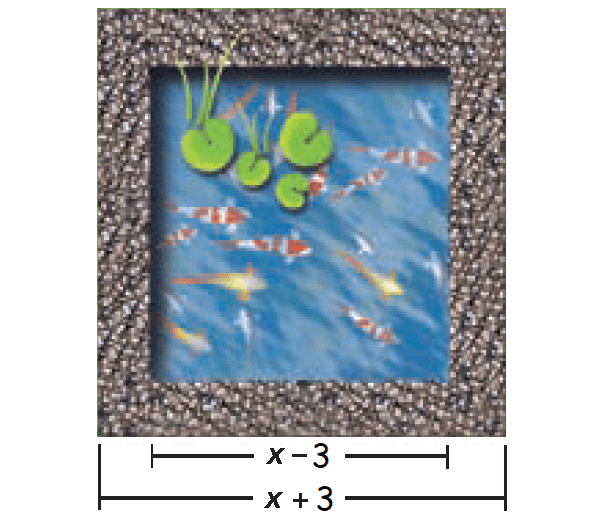
Understand the Problem.

The answer will be an expression that represents the area of the path.

List the important information :

(i) The pond is a square with a side length of (x - 3).

(ii) The path has a side length of (x + 3).

Make a Plan.

The area of the pond is (x - 3)². The total area of the path plus the pond is (x + 3)². You can subtract the area of the pond from the total area to find the area of the path.

Solve.

Step 1 :

Find the total area.

Use the rule for (a + b)².

(a + b)² = a² + 2ab + b²

Identify a and b : a = x and b = 3.

(x + 3)² = (x)² + 2(x)(3) + (3)²

= x² + 6x + 9

Step 2 :

Find the area of the pond.

Use the rule for (a - b)².

(a - b)² = a² - 2ab + b²

Identify a and b : a = x and b = 3.

(x - 3)² = (x)² - 2(x)(3) + (3)²

= x² - 6x + 9

Step 3 :

Find the area of the path.

Area of Path = Total Area - Area of Pond

= (x² + 6x + 9) - (x² - 6x + 9)

Use the Distributive Property.

= x² + 6x + 9 - x² + 6x - 9

Group like terms together.

= (x² - x²) + (6x + 6x) + (9 - 9)

Combine like terms.

= 12x

The area of the path is 12x.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.