SOLVING WORD PROBLEMS USING SYSTEMS OF EQUATIONS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
A problem involving two unknown quantities can be solved by using a system of equations.
Plan for Solving a Word Problem :
(i) Find out what numbers are asked for from the given information.
(ii) Choose variables to represent the numbers described in the problem. Sketch or a chart may be helpful.
(iii) Write the system of equations that represents relationships among the numbers in the problem.
(iv) Solve the system of equations and find the required numbers.
(v) Answer the original question. Check that your answer is reasonable.
Problem 1 :
Adam and Betty purchased a printer together for $258. If Adam paid $18 less than twice Betty, how much money did Adam pay for the printer?
Solution :
Let a be the price of the printer for Adam and b be the price of the printer for Betty.
From the given information, we have
a + b = 258 ----(1)
a = 2b - 18 ----(2)
Substitute a = 2b - 18 into (1).
2b - 18 + b = 258
3b - 18 = 258
3b = 276
b = 92
Substitute b = 92 into (2).
a = 2(92) - 18
a = 184 - 18
a = 166
Adam paid $166 for the printer.
Problem 2 :
There are 28 tables for customers at Mesa Grill Restaurant. The tables are either two-seat tables or four-seat tables. When all the tables are full, there will be 90 customers in the restaurant. How many two-seat tables are at the restaurant?
Solution :
Let t be the number of two-seat tables f be the number of four-seat tables.
From the given information, we have
t + f = 28 ----(1)
2t + 4f = 90 ---> t + 2f = 45 ----(2)
Subtract (1) from (2) to get rid od t.
(2) - (1) :
(t + 2f) - (t + f) = 45 - 28
t + 2f - t - f = 17
f = 17
Substitute f = 17 into (1).
t + 17 = 28
t = = 11
There are 11 two-seat tables in the restaurant.
Problem 3 :
In a basketball, a field goal is either 2 or 3 points. In a college basketball tournament, Jim made 73 more 2-point field goals than 3-point field goals. If he scored a total of 216 goals in the tournament how many 3-point field goals did he make?
Solution :
Let Jim make x number of 2-point and y number of 3-point field goals.
From the given information, we have
x = y + 73 ----(1)
2x + 3y = 216 ----(2)
Substitute x = y + 73 into (2).
2(y + 73) + 3y = 216
2y + 146 + 3y = 216
5y + 146 = 216
5y = 70
y = 14
Number of 3-point field goals made by Jim is 14.
Problem 4 :
In a car dealership, all of the vehicles are either a sedan or a SUV. If 36 sedans are sold and 36 SUVs are added, there will be an equal number of sedans and SUVs. If 8 SUVs are sold and 8 sedans are added, there will be twice as many sedans as SUVs. How many sedans were at the dealership before any vehicle was sold?
Solution :
Let x be the original number of sedans and y be the oriinal number of SUVs.
Given : If 36 sedans are sold and 36 SUVs are added, there will be an equal number of sedans and SUVs.
x - 36 = y + 36
x = y + 72 ----(1)
Given : If 8 SUVs are sold and 8 sedans are added, there will be twice as many sedans as SUVs.
x + 8 = 2(y - 8) ----(2)
Substitute x = y + 72 into (2).
y + 72 + 8 = 2(y - 8)
y + 80 = 2y - 16
y = 96
Substitute y = 96 into (1).
x = 96 + 72
x = 168
There were 168 sedans originally in the store.
Problem 5 :
At a coffee shop, a 16 ounce bag of coffee is on sale at $5.25 less than the regular price. The cost of 4 bags of coffee at regular price is the same as the cost of 6 bags of coffee at sale price. Let r be the regular price of coffee and s be the sale price of coffee. Which of the following systems of equations can be used to find the values of variables r and s?
(A) s = r - 16 and r = 6s
(B) s = r - 5.25 and 4r = 16
(C) s = r - 5.25 and 4r = 6s
(D) s = r + 5.25 and 4r = 6s
Solution :
r ---> regular price
s ----> sale price
Given : A 16 ounce bag of coffee is on sale at $5.25 less than the regular price.
s = r - 5.25 ----(1)
Given : The cost of 4 bags of coffee at regular price is the same as the cost of 6 bags of coffee at sale price.
4r = 6s ----(2)
The system of equations can be used to find the values of
variables r and s :
s = r - 5.25
4r = 6s
Problem 6 :
At a museum, Lily bought 3 student tickets and 2 adult tickets for $29.00. At the same museum Samantha bought 5 student tickets and 4 adult tickets for $54.00. How much does one student ticket and one adult ticket cost?
Solution :
Let 's' be the price of the student ticket and 'a' be the price of the adult ticket.
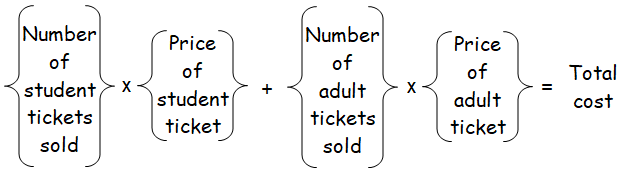
|
First equation : 3s + 2a = 29 ----(1) |
Second equation : 5s + 4a = 54 ----(2) |
Multiply the by -2.
-6s - 4a = -58 ----(3)
(3) + (2) :
-s = -4
Multiply each side by -1.
s = 1
Substitute s = 1 in (1).
3(4) + 2a = 29
12 + 2a = 29
Subtract 12 from each side.
2a = 17
Divide each side by 2.
a = 8.5
Add the values of 's' and 'a'.
s + a = 4 + 8.5
s + a = 12.5
The cost of one student ticket and one adult ticket is $12.50.
Problem 7 :
On the second weekend of July, Alex hiked 10 less than twice the number of miles that he hiked on the first weekend of July. In these two weeks he hiked a total of 38 miles. How many miles did he hike on the first weekend?
Solution :
The problem asks for the number of miles Alex hiked on the first week of July.
Let 'x' be the number of miles Alex hiked on the first week and 'y' be the number of miles Alex hiked on the second week.
Number of miles hiked on the second weekend
=
10 miles less than twice the number of miles he hiked on the first weekend
Total number of miles hiked in the two weekends is 38.
|
First equation : y = 2x - 10 ----(1) |
Second equation : x + y = 38 ----(2) |
Substitute (2x - 10) for y in (2).
x + (2x - 10) = 38
x + 2x - 10 = 38
3x - 10 = 38
Add 10 to each side.
3x = 48
Divide each side by 3.
x = 16
Alex hiked 16 miles on the first weekend.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 45)
Jan 19, 26 06:14 AM
10 Hard SAT Math Questions (Part - 45) -
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations
