SOLVING WORD PROBLEMS USING SUBSTITUTION METHOD
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
We use the following steps to solve a system of linear equations.
Step 1 :
Solve one of the equations for one of its variables.
Step 2 :
Substitute the expression from step 1 into the other equation and solve for the other variable.
Step 3 :
Substitute the value from step 2 into either original equations and solve for the variable in step 1.
Problem 1 :
Solve 2x + 3y = 11 and 2x - 4y = -24 and hence find the value of "m" for which y = mx + 3.
Solution :
2x + 3y = 11 ----------- (1)
2x - 4y = -24 ----------- (2)
Step 1 :
Find the value of one variable in terms of other variable
3y = 11 - 2 x
y = (11 - 2 x)/3
Let us apply the value of y in (2),
2x - 4(11 - 2x)/3 = -24
14x - 44 = -24 (3)
14x - 44 = -72
14x = -72 + 44
14x = - 28
Divide 14 on both sides, we get
x = -2
Substitute x = -2 in the equation y = (11 - 2 x)/3
y = [11 - 2(-2)]/3
y = 15/3
y = 5
Now we have to apply these values in the equation
y = m x + 3
5 = m (-2) + 3
5 = -2 m + 3
-2m = 2
-2 m = 2
m = 2/(-2)
m = -1
Problem 2 :
The difference between two numbers is 26 and one number is three times the other. Find them
Solution :
Let the two numbers are "x" and "y"
Difference between two number is 26
x - y = 26 -------- (1)
One number is three times the other
x = 3 y -------- (2)
Let us apply (2) in (1)
3 y - y = 26
2 y = 26
Divide by 2 on both sides, we get
y = 13
By applying the value of y in (2), we get
x = 3 (13)
x = 39
So, required two numbers are 39 and 13.
Problem 3 :
The larger of two supplementary angles exceeds the smaller by 18 degrees. Find them
Solution :
Let the two supplementary angles are "x" and "y"
Sum of these two angles is 180
x + y = 180 -----(1)
the larger angle exceeds the smaller by 18
x = y + 18 -----(2)
Now, we are going to apply the value of x in the first equation
y + 18 + y = 180
2y = 180 - 18
2y = 162
y = 162/2
y = 81
x = 81 + 18
x = 99
So, two supplementary angles are 99 and 81.
Problem 4 :
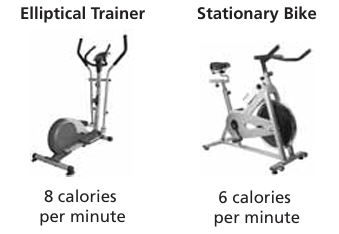
You have 40 minutes to exercise at the gym, and you want to burn 300 calories total using both machines. How much time should you spend on each machine?
Solution :
Let x be the number of minutes you spend in Elliptical trainer.
Let y be the number of minutes you spent in stationary bike.
x + y = 40 ------(1)
8x + 6y = 300------(2)
From (1), y = 40 - x
Applying the value of y in (2), we get
8x + 6(40 - x) = 300
8x + 240 - 6x = 300
2x = 300 - 240
2x = 60
x = 30
Applying the value of x in y = 40 - x
y = 40 - 30
y = 10
You spent 30 minutes in Elliptical trainer and 10 minutes in stationary bike.
Problem 5 :
The sum of the digits of a two-digit number is 11. When the digits are reversed, the number increases by 27. Find the original number
Solution :
Let xy be the required two digit number. Sum of the digits = 11
x + y = 11 -----(1)
When digits are reversed, then xy will become yx.
yx = xy + 27
10y + 1x = 10x + 1y + 27
1x - 10x + 10y - 1y = 27
-9x + 9y = 27
Dividing by 9, we get
-x + y = 3 -----(2)
y = x + 3
Applying the value of y in (1), we get
x + x + 3 = 11
2x = 11 - 3
2x = 8
x = 4
y = 4 + 3
y = 7
So, the required two digit number is 47.
Problem 6 :
A radio station plays a total of 272 pop, rock, and hip-hop songs during a day. The number of pop songs is 3 times the number of rock songs. The number of hip-hop songs is 32 more than the number of rock songs. How many of each type of song does the radio station play?
Solution :
Let x be the number of rock songs and y be the number of pop songs.
y = 3x --------(1)
Number of hip-hop songs = x + 32
x + y + x + 32 = 272
2x + y = 272 - 32
2x + y = 240 --------(2)
Applying the value of y in (2), we get
2x + 3x = 240
5x = 240
x = 240/5
x = 48
y = 3(48)
y = 144
Number of rock songs = 48
Number of pop songs = 144
Number of hip-hop songs = 48 + 32 ==> 80
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4) -
10 Hard SAT Math Questions (Part - 3)
Jan 05, 26 06:34 PM
10 Hard SAT Math Questions (Part - 3)

