SOLVING WORD PROBLEMS USING PYTHAGOREAN THEOREM

Example 1 :

A rectangle has length 6 cm greater than its width. Find its width given that its area is 91 cm²

Solution :

Let, width  =  x cm and length  =  (x+6) cm

Area  =  91 cm²

Area of a rectangle  =  length × width

x (x + 6)  =  91

x² + 6x – 91  =  0

By factorization, we get

(x + 13) (x – 7)  =  0

x + 13  =  0 or x – 7  =  0

x  =  - 13 or x  =  7

Since the side length cannot be considered with negative sign. Width can be 7 cm.

Example 2 :

A triangle has base 2 cm more than its altitude. If its area is 49.5 cm², find its altitude.

Solution :

Let, altitude  =  x cm and base  =  (x + 2) cm

Area  =  49.5 cm²

Area of a triangle  =  1/2 (base × altitude)

1/2 [(x+2) . x]  =  49.5

1/2 (x²+2x)  =  49.5

x²+2x  =  (49.5 × 2)

x² + 2x  =  99

x² + 2x – 99  =  0

By factorization, we get

(x + 11) (x – 9)  =  0

x + 11  =  0 or x – 9  =  0

x  =  - 11 or x  =  9

we taking positive value x  =  9 cm

altitude  =  9 cm

So, its altitude is 9 cm.

Example 3 :

A rectangular enclosure is made from 40 m of fencing. The area enclosed is 96 m². Find the dimensions of the enclosure.

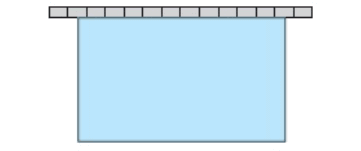
Solution :

Let, length  =  x m and width  =  y m of rectangular enclosure.

If perimeter is 40 m

Perimeter of rectangle  =  2(l + w)

2(x + y)  =  40

x + y  =  20 -----(1)

Area  =  96 m²

xy  =  96

y  =  96/x -----(2)

By applying y  =  96/x in equation (1), we get

x + 96/x  =  20

x² + 96  =  20x

x² – 20x + 96  =  0

By factorization, we get

(x – 12) (x – 8)  =  0

x  =  12 m or 8 m

x  =  12 m

Now, length x  =  12 m

By applying x  =  12 m in equation (1), we get

y  =  96/x

y  =  96/12

y  =  8 m

width y  =  8 m

So, dimensions of the enclosure 12 m × 8 m

Example 4  :

Use the theorem of Pythagoras to find x given :

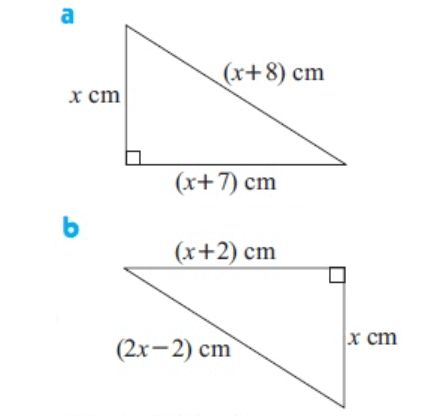
Solution :

By using Pythagorean theorem,

AB² + BC²  =  AC²

x²+(x+7)²  =  (x+8)²

x²+x²+14x+49  =  x²+16x+64

2x²+14x+49–x²–16x–64  =  0

x²–2x–15  =  0

By factorization, we get

(x–5) (x+3)  =  0

x  =  5 or – 3

So, the value of x is 5

b)  By using Pythagorean theorem,

AB² + BC²  =  AC²

(x+2)² + x²  =  (2x-2)²

x²+4x+4+x²  =  4x²-8x+4

2x²+4x+4–4x²+8x–4  =  0

- 2x² + 12x  =  0

- 2x(x - 6)  =  0

x - 6  =  0

Now, x  =  6

So, the value of x is 6

Example 5 :

A right angled triangle has sides 2 cm and 9 cm respectively less than its hypotenuse. Find the length of each side of the triangle.

Solution :

Let x  =  hypotenuse c,

then a  =  (x–2) cm and b  =  (x–9) cm

In right angled triangle, using Pythagorean theorem

a²+b²  =  c²

(x–2)² + (x–9)²  =  x²

x²-4x+4+x²-18x+81  =  x²

2x²–22x+85–x²  =  0

x²–22x+85  =  0

By factorization, we get

(x–5) (x–17)  =  0

x  =  5 or 17

In any right triangle hypotenuse is the longest side. So, we take x as 17 cm.

hypotenuse c  =  17 cm

then a  =  (x – 2) cm

a  =  15 cm

b  =  (x–9) cm

b  =  8 cm

So, each side of the triangle are 8 cm, 15 cm, 17 cm.

Example 6 :

A gardener plants 600 cabbage in rows. If the number of cabbages in each row is 10 more than twice the number of rows, how many rows did the gardener plant ?

Solution :

Let x  =  number of rows

The number of cabbage in each row is 10 + 2x

Total number of cabbage is 600, then

x(10 + 2x)  =  600

10x + 2x²  =  600

2x² + 10x – 600  =  0

x² + 5x – 300  =  0

(x + 20) (x – 15)  =  0

x  =  - 20 or 15

x  =  15 rows

So, the number of rows is 15

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.