SOLVING WORD PROBLEMS USING GRAPHICAL METHOD

Problem 1 :

Half the perimeter of a rectangular garden, whose length is 4 m more its width is 36 m. Find the dimensions of the garden.

Solution :

Let "x" be the width of the rectangular garden

Let "y" be its length

y = x + 4  -------- (1)

Half the perimeter of the rectangular garden = 36 m

perimeter of rectangle = 2 (L + b)

L + b = 36

y + x = 36

y = 36 - x -------- (2)

Now let us find x and y intercepts to draw the graph.

Graphing 1^st line :

y = x + 4 

Graphing 2^nd line :

y  =  36 - x

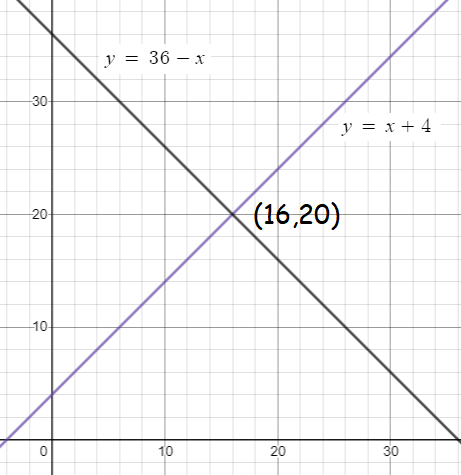
Thew above lines are intersecting at the point (16, 20). So, length of the rectangular garden is 20 m and width of the rectangular garden is 16 m.

Problem 2 :

Given the linear equation 2 x + 3 y - 8 = 0, write another linear equation in two variables such that the geometrical representation of the pair so formed is:

Solution :

(i) intersecting lines

The condition for intersecting lines is a₁/a₂ ≠ b₁/b₂.

According to the above condition, we have to form an equation.

 a₁ = 2          b₁ = 3            c₁ = -8

The values of a₂,b₂ and c₂ be any real values but the simplified values of a₁/a₂ and b₁/b₂ shouldn't be equal.

 a₂ = 3         b₂ = -3            c₂ = -16

So,  one of the required possible equation is

3x - 3y - 16 = 0.

(ii) Parallel lines

The condition  for two parallel lines is a₁/a₂ = b₁/b₂ ≠ c₁/c₂. According to the above condition, we have to form a equation.

 a₁ = 2          b₁ = 3            c₁ = -8

if the value of a₂ is 4, the value of b₂ will be 6. The value of c₂ must be any value other than -16. 

 a₂ = 4         b₂ = 6            c₂ = 6

So one of the required possible equation is

4x + 6y - 6 = 0.

(iii) Coincident lines

The condition  for coincident lines is a₁/a₂ = b₁/b₂ = c₁/c₂.According to the above condition,we have to form a equation.

  a₁ = 2          b₁ = 3            c₁ = -8

the values of a₂, b₂ and c₂ will be 

 a₂ = 4         b₂ = 6            c₂ = -16

So one of the required possible  equation is

4x + 6y - 16 = 0.

use the graph to solve the system of linear equations. Check your solution.

Problem 3 :

x - y = 4

4x + y = 1

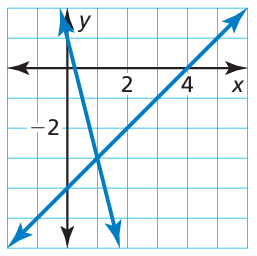
Solution :

x - y = 4 ----(1)

4x + y = 1 ----(2)

y = x - 4

Applying y in (2), we get

4x + x - 4 = 1

5x = 1 + 4

5x = 5

x = 1

Applying x = 1, we get

y = 1 - 4

y = -3

The solution for the system of linear equations is (1, -3)

By observing the graph, the point of intersecting is (1, -3). Then the answer is correct.

Problem 4 :

x + y = 5

y - 2x = -4

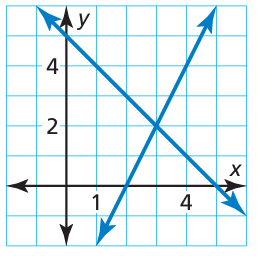
Solution :

x + y = 5 -----(1)

y - 2x = -4 -----(2)

y = 5 - x

Applying the value of y in (2), we get

5 - x - 2x = -4

-3x = -4 - 5

-3x = -9

x = 3

Applying the value of y in y = 5 - x 

y = 5 - 3

y = 2

The point of intersection from the graph is (3, 2). The solution from the calculation is also (3, 2). So, the answer is correct.

use only the slopes and y-intercepts of the graphs of the equations to determine whether the system of linear equations has one solution, no solution, or infinitely many solutions. Explain. 

Problem 5 :

y = 7x + 13

-21x + 3y = 39

Solution :

y = 7x + 13 ------(1)

-21x + 3y = 39 ------(2)

By comparing the slopes and y-intercepts, we can decide the lines should have what type of solution.

Since the slope and y-intercepts are equal, the must be co-incident or overlapping lines. They must have infinite number of solutions.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.