SOLVING WORD PROBLEMS USING CRAMER'S RULE

In this section, you will learn how to solve word problems using Cramer's rule. 

Let us consider the following system of three equations with three unknowns x, y and z. 

a₁₁x + a₁₂y + a₁₃z  =  b₁

a₂₁x + a₂₂y + a₂₃z  =  b₂

a₃₁x + a₃₂y + a₃₃z  =  b₁

Now, we can write the the following determinants using the above equations. 

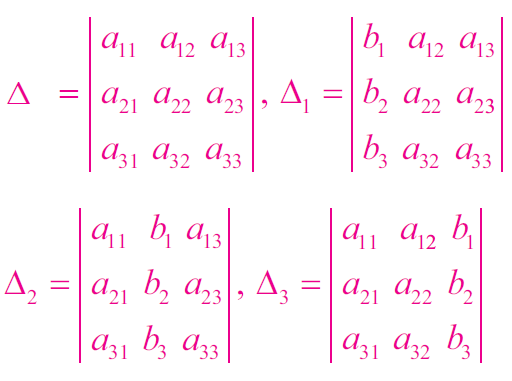
Then, Cramer’s rule to find the values of x, y and z :

x  =  Δ₁/Δ

y  =  Δ₂/Δ

z  =  Δ₃/Δ

If Δ  =  0, the system is inconsistent and it has solution. 

Problem 1 :

In a competitive examination, one mark is awarded for every correct answer while 1/4 mark is deducted for every wrong answer. A student answered 100 questions and got 80 marks. How many questions did he answer correctly ? (Use Cramer’s rule to solve the problem).

Solution :

Total numbers of questions  =  100

Let "x" and "y" be the number of questions answered correctly and incorrectly respectively.

Then, 

x + y  =  100

1x - (1/4) y  =  80

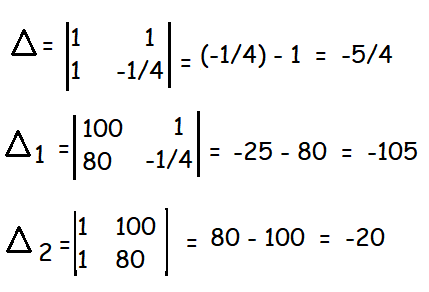
By Cramer's rule,

x₁  =  Δ₁/Δ

x  =  -105/(-5/4)

x  =  105(4/5)

  x  =  84

y  =  Δ₂/Δ

y  =  -20/(-5/4)

y  =  20(4/5)

y  =  16

So, the number of questions answered correctly is 84 and wrongly is 16.

Problem 2 :

A chemist has one solution which is 50% acid and another solution which is 25% acid. How much each should be mixed to make 10 litres of a 40% acid solution ? (Use Cramer’s rule to solve the problem).

Solution :

Let "x" and "y" be the quantity of 1st and second solution.

Then, 

x + y  =  10 -----(1)  

50% of x + 25% of y  =  40% of 10

0.5x + 0.25y  =  4 -----(2)

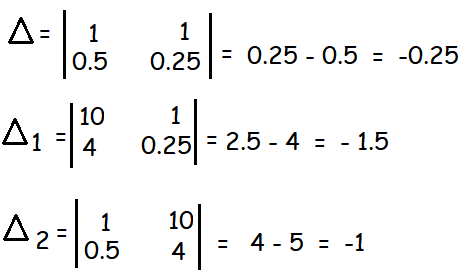
By Cramer's rule,

x₁  =  Δ₁/Δ

x  =  -1.5/(-0.25)

x  =  6

y  =  x₂ = Δ₂/Δ  =  -1/(-0.25)

=  4

So, the quantity of 1st solution is 6 liters and second solution is 4 liters.

Problem 3 :

A fish tank can be filled in 10 minutes using both pumps A and B simultaneously. However, pump B can pump water in or out at the same rate. If pump B is inadvertently run in reverse, then the tank will be filled in 30 minutes. How long would it take each pump to fill the tank by itself ? (Use Cramer’s rule to solve the problem).

Solution :

Let "x" be the number of minutes taken by sump A to fill the tank.

Let "y" be the number of minutes taken by sump B to fill the tank.

A pump fill in 1 min  = 1/x

B pump fill in 1 min = 1/y

A& B together in 1 min = 1/x + 1/y

1/x + 1/y  =  1/10 -----(1)

1/x - 1/y  =  1/30 -----(2)

1/x  =  a and 1/y  =  b

a + b  =  1/10 -----(1)

a - b  =  1/30 -----(2)

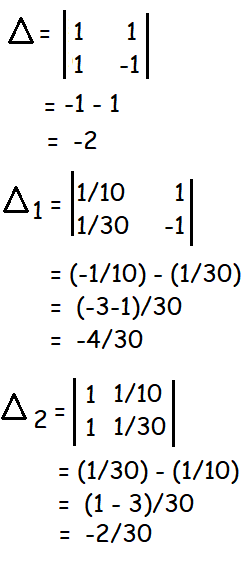
By Cramer's rule,

x  =  Δ₁/Δ

  x  =  (-4/30)/(-2)

x  =  1/15

y  =  Δ₂/Δ

y  =  (-2/30)/(-2)

y  =  1/30

A alone can fill in 15 mins

B alone can fill in 30 mins

Problem 4 :

A family of 3 people went out for dinner in a restaurant. The cost of two dosai, three idlies and two vadais is ₹ 150. The cost of the two dosai, two idlies and four vadais is ₹200. The cost of five dosai, four idlies and two vadais is ₹250. The family has ₹350 in hand and they ate 3 dosai and six idlies and six vadais. Will they be able to manage to pay the bill within the amount they had ?

Solution :

Let "x", "y" and "z" be the cost of 1 dosa, 1 idly and 1 vada respectively.

2x + 3y + 2z  =  150

2x + 2y + 4z  =  200

5x + 4y + 2z  =  250

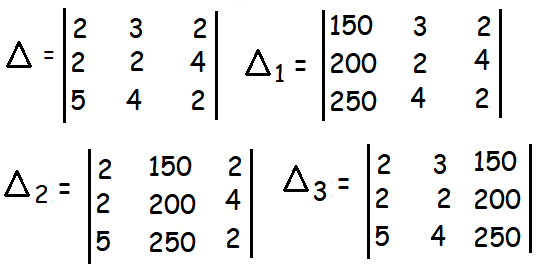
Δ  =  2(4 - 16) - 3(4 - 20) + 2(8 - 10)

  =  2(-12) - 3(-16) + 2(-2)

  =  -24 + 48 - 4

  =  -28 + 48

Δ  =  20

Δ₁  =  150(4 - 16) - 3(400 - 1000) + 2(800 - 500)

  =  150(-12) - 3(-600) + 2(300)

  = -1800 + 1800 + 600

Δ₁  =  600

Δ₂  =  2(400 - 1000) - 150(4 - 20) + 2(500 - 1000)

  =  2(-600) - 150(-16) + 2(-500)

  =  -1200 + 2400 - 1000

Δ₂  =  200

Δ₃  =  2(500 - 800) - 3(500 - 1000) + 150(8 - 10)

  =  2(-300) - 3(-500) + 150(-2)

  =  -600 + 1500 - 300

Δ₃  =  600

By Cramer's rule, 

x  =  Δ₁/Δ  =  600/20  =  30

y  =  Δ₂/Δ  =  200/20  =  10

z  =  Δ₃/Δ  =  600/20  =  30

So, cost of 1 ildy  = ₹30, cost of 1 dosa = ₹10 and cost of 1 vada = ₹30.

3x + 6y + 6z :  

=  3(30) + 6(10) + 6(30)

=  90 + 60 + 180

 =  330

So, the amount is enough to pay the bill.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.