SOLVING WORD PROBLEMS INVOLVING VOLUME OF CUBES

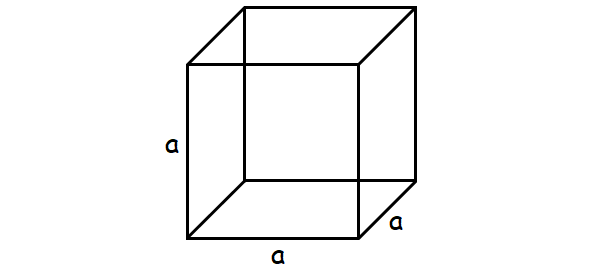
Formula : 

Volume of a cube = a³ cubic units

Problem 1 :

Find the volume of a cube each of whose side is (i) 5 cm (ii) 3.5 m (iii) 21 cm

Solution :

(i) 5 cm :

Volume of cube = a³

= 5³

= 125 cm³

(ii) 3.5 m :

= 3.5³

= 42.875 cm³

(iii) 21 cm :

= 21³

= 9261 cm³

Problem 2 :

A cubical milk tank can hold 125000 liters of milk. Find the length of its side in meters.

Solution :

Volume of cubical milk tank = 125000 liters

1000 liters = 1 m³,

Volume of tank = 125000/1000

a³ = 125

a = 5 m

Problem 3 :

A metallic cube with side 15 cm is melted and formed into a cuboid. If the length and height of the cuboid is 25 cm and 9 cm respectively then find the with of the cuboid.

Solution :

volume of cuboid = volume of cube

l x w x h = a³

25 x w x 9 = 15³

225w = 3375

Divide each side by 225.

w = 15 cm

Problem 4 :

The sides of two cubes A and B are in the ratio 3 : 5. If the volume of cube A is 729 cm³, find the volume of cube B. 

Solution :

From the ratio 3 : 5, the sides of cubes A and B are 

3x, 5x

Volume of cube A = 243 cm³

(3x)³ = 729

27x³ = 729

Divide each side by 27.

x³ = 27

x³ = 3³

x = 3

Side of cube A = 3(3) = 9 cm

Side of cube B = 5(3) = 15 cm

Volume of cube B : 

= 15³

= 3375 cm³

Problem 5 :

If the sides of two cubes are in the ratio 4 : 7, find the ratio of their volumes. 

Solution :

From the ratio 4 : 7, the sides of two cubes are 

4x, 7x

Ratio of their volumes :

= (4x)³ : (7x)³

= 64x³ : 343x³

Divide both the terms of the ratio by x³.

= 64 : 343

Problem 5 :

The solid triangular prism shown below is made from metal. The prism is melted down and the metal is used to create a solid cube. Find the side length of the cube.

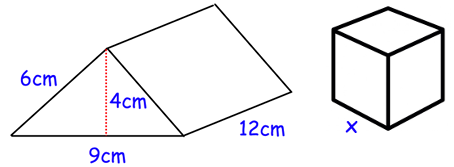
Solution :

Volume of triangular prism = volume of cube

area of triangle x height = x³

base of triangle = 9 cm, height of triangle = 4 cm and height of prism = 12 cm

(1/2) x 9 x 4 x 12 = x³

216 = x³

x³ = 6³

x = 6

So, the side length of cube is 6 cm.

Problem 5 :

Two cubes, each of side 6 cm, are joined end to end. Find the volume of the to end.

Solution :

Side length of cube = 6 cm

After joining two cubes together, length of cuboid = 12 cm

width = 6 cm and height = 6 cm

Volume of cuboid = length x width x height

= 12 x 6 x 6

= 432 cm³

Problem 6 :

Find the volume of the How many 8 cm cubes can be cut out from the cube whose edge is 32 cm?

Solution :

Number of cubes to be cut

= volume of cube whose edge is 32 cm/volume of cube whose edge is 8 cm

= (32 x 32 x 32) / (8 x 8 x 8)

= 64 cubes.

Problem 7 :

A cuboid is of dimensions 60 cm x 54 cm x 30 cm. How many small cubes of side 6 cm can be placed in the given cuboid.

Solution :

Volume of cuboid = length x width x height

= 60 x 54 x 30

= 97200

Volume of cube = 6 x 6 x 6

= 216

Number small cubes to be cut = 97200 / 216

= 450 cubes

Problem 8 :

A cube of side 5 cm is cut into 1 cm cubes. Find the percentage increase in volume after such cutting.

Solution :

Volume of cube whose side is 5 cm

= 5 x 5 x 5

= 125

Volume of cube whose side is 1 cm

= 1 x 1 x 1

= 1

Percentage increase = [(125 - 1)/125] x 100%

= (124 / 125) x 100%

= 99.2%

Problem 9 :

A cuboid is 40 cm x 20 cm x 10 cm. What would be the side of a cube having the same volume?

a) 20 cm     b) 40 cm    c) 10 cm      d) 30cm

Solution :

Volume of cuboid = volume of cube

Side length of cube be x.

40 x 20 x 10 = x³

8000 = x³

x³ = 20³

Side length of cube is 20 cm.

Problem 10 :

If each side of a cube is doubled then its volume

a) is doubled       b) becomes 4 times

c) becomes 6 times    d) becomes 8 times

Solution :

Let x be the side, then 2x be the after the side is doubled.

volume of cube whose side length is x cm

= x³

Volume of cube whose side length is 2x

= (2x)³

= 8x³

The new volume becomes 8 times of the old.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.