SOLVING VOLUME EQUATIONS

We can use the formula for the volume of a rectangular prism to write an equation. Then solve the equation to find missing measurements for a prism.

Example 1 :

Samuel has an ant farm with a volume of 375 cubic inches. The width of the ant farm is 2.5 inches and the length is 15 inches. What is the height of Samuel’s ant farm?

Solution :

From the given information, it is clear that the shape of ant form is rectangular prism.

Let us write formula for volume of rectangular prism (ant form)

V  =  l x w x h 

Use the formula to write an equation.

Substitute V  =  375, w  =  2.5 and l  =  15.

375  =  15 x 2.5 x h

375  =  37.5 x h

Divide each side 37.5.

10  =  h

So, the height of the form is 10 inches. 

Example 2 :

A terrarium is shaped like a rectangular prism with a volume of 5200 cubic inches. The prism is 13 inches wide and 16 inches deep. Find the length of the terrarium.

Solution :

From the given information, we can have the following figure. 

Let us write formula for volume of rectangular prism. 

V  =  l x w x h 

Use the formula to write an equation.

Substitute V  =  5200, w  =  13 and h  =  16.

5200  =  l x 13 x 16

5200  =  l x 208

Divide each side by 208.

25  =  l

So, the length of terrarium is 25 inches. 

Example 3 :

A rectangular swimming pool is in shape of rectangular prism with a volume of 393 3/4 cubic meters. The swimming pool is 15 meters long and 2 1/2 meters deep. Find the width of the pool.

Solution :

From the given information, we can have the following figure. 

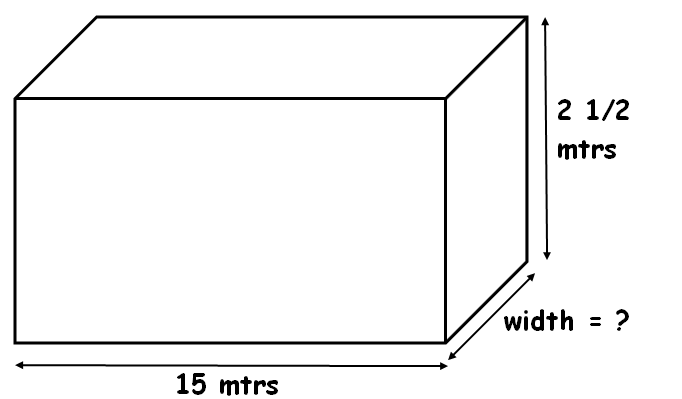
Let us write formula for volume of rectangular prism. 

V  =  l x w x h

Use the formula to write an equation.

Substitute V  =  393 3/4, l  =  15 and h  =  2 1/2.

393 3/4  =  15 x w x 2 1/2

1575/4  =  15 x w x 5/2

1575/4  =  w x 75/2

Multiply each side by 2/75.

21/2  =  w

10 1/2  =  w

So, the width of the swimming pool is 10 1/2 meters. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.