SOLVING SYSTEMS OF LINEAR EQUATIONS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
A set of linear equations with the same two variables is called a system of linear equations. We can solve a system of linear equations with two variables using one of the following two methods.
Solving Linear Systems by Substitution
The basic steps in the substitution method are as follows:
Step 1 :
Solve one of the equations for one of its variables.
Step 2 :
Substitute the resulting expression into the other equation and solve.
Step 3 :
Substitute the resulting value into either of the original equations and solve for the other variable.
Solve the linear systems by substitution method.
Example 1 :
y = x - 1
2x + y = 5
Solution :
y = x - 1 ----(1)
2x + y = 5 ----(2)
Substitute y = x - 1 in (2).
2x + (x - 1) = 5
2x + x - 1 = 5
3x - 1 = 5
Add 1 to both sides.
3x = 6
Divide both sides by 3.
x = 2
Substitute x = 2 in (1).
y = 2 - 1
= 1
The solution is (x, y) = (2, 1).
Example 2 :
-2x + y = 4
x - y = -1
Solution :
Solve for y in -2x + y = 4.
-2x + y = 4
Add 2x to both sides.
y = 4 + 2x ----(1)
x - y = -1 ----(2)
Substitute y = 4 + 2x in (2).
x - (4 + 2x) = -1
x - 4 - 2x = -1
-x - 4 = -1
Add 4 to both sides.
-x = 3
Multiply both sides by -1.
x = -3
Substitute x = -3 in (1).
y = 2(-3) + 4
= -6 + 4
= -2
The solution is (x, y) = (-3, -2).
Example 3 :
x - 2y = 1
3x + 5y = 14
Solution :
Solve for x in x - 2y = 1.
x - 2y = 1
Add 2y to both sides.
x = 1 + 2y ----(1)
3x + 5y = 14 ----(2)
Substitute x = 1 + 2y in (2).
3(1 + 2y) + 5y = 14.
3 + 6y + 5y = 14
3 + 11y = 14
Subtract 3 from both sides.
11y = 11
Divide both sides by 11.
y = 1
Substitute y = 1 in (1).
x = 1 + 2(1)
= 1 + 2
= 3
The solution is (x, y) = (3, 1).
Example 4 :
The age of a father is three more than two times the age of his son. If the sum of ages of the father and son is equal to 78, find their ages.
Solution :
Let f and s be the ages of father and son respectively.
f = 2s + 3 ----(1)
f + s = 78 ----(2)
Substitute f = 2s + 3 in (2).
2s + 3 + s = 78
3s + 3 = 78
Subtract 3 from both sides.
3s = 75
Divide both sides by 3.
s = 25
Substitute s = 25 in (1).
f = 2(25) + 3
f = 50 + 3
f = 53
The age of the father is 53 years and that of the son is 25 years.
Solving Linear Systems by Elimination
The basic steps in the elimination method are as follows :
Step 1 :
Arrange the equations with the like terms in columns.
Step 2 :
Multiply one or both equations to obtain new coefficients for x (or y) that are opposites.
Step 3 :
Add the equations and solve for the remaining variable.
Step 4 :
Substitute this value into either of the original equations and solve for the other variable.
Solve the linear systems by elimination method.
Example 1 :
2x - 3y = 1
5x + 3y = 13
Solution :
In the given system of linear equations, we have the same coefficient for y with different signs. By adding the two equations, y can be eliminated.
2x - 3y = 1 ----(1)
5x + 3y = 13 ----(2)
(1) + (2) :
7x = 14
Divide both sides by 7.
x = 2
Substitute x = 2Divide both sides by 3.
x = 2
Substitute x = 2 in (1).
2(2) - 3y = 1
4 - 3y = 1
Subtract 4 from both sides.
-3y = -3
Divide both sides by -3.
y = 1
The solution is (x, y) = (2, 1).
Example 2 :
5x + 6y = 17
3x - 4y = -5
Solution :
5x + 6y = 17 ----(1)
3x - 4y = -5 ----(2)
In the given system of linear equations, both the variables x and y do not have the same coefficient. If we want to eliminate y, it must have the same coefficient with different signs. We can make the coefficient of y same in both the equations using least common multiple.
Least common multiple of (6, 4) = 12.
(1) x 2 + (2) x 3 :
19x = 19
Divide both sides by 19.
x = 1
Substitute x = 1 in (1).
5(1) + 6y = 17
5 + 6y = 17
Subtract 5 from both sides.
6y = 12
Divide both sides by 6.
y = 2
The solution is (x, y) = (1, 2).
Example 3 :
x - 5y = -2
3x + 2y = 11
Solution :
x - 5y = -2 ----(1)
3x + 2y = 11 ----(2
In the given system of linear equations, both the variables x and y do not have the same coefficient. If we want to eliminate x, it must have the same coefficient with different signs. We make the coefficient of x same in both the equations by multiplying the first equation by 3.
(1) x 3 - (2) ;
-17y = -17
Divide both sides by -17.
y = 1
Substitute y = 1 in (1).
x - 5(1) = -2
x - 5 = -2
Add 5 to both sides.
x = 3
The solution is (x, y) = (3, 1).
Example 4 :
A park charges $10 for adults and $5 for kids. How many many adults tickets and kids tickets were sold, if a total of 548 tickets were sold for a total of $3750 ?
Solution :
Let x and y be the number of adult kids tickets sold respectively.
Given :A total of 548 tickets were sold.
x + y = 548 ----(1)
Given : Cost of each adult ticket is $10 and kid ticket is $5 and tickets were sold for a total of $3750.
10x + 5y = 3750
Divide both sides by 5.
2x + y = 750 ----(2)
In (1) and (2), we have the same coefficient for y. By subtracting the equation, we can eliminate y.
(2) - (1) :
x = 202
Substitute x = 202 in (1).
202 + y = 548
Subtract 202 from both sides.
y = 346
Hence, the number of adults tickets sold is 202 and kids tickets is 346.
Linear System with One Solution
The graph of a linear equation in two variables is always a straight line.
We get two straight lines from a system of two linear equations with two variables each..
If the two lines intersect at one point, then the system has one solution.
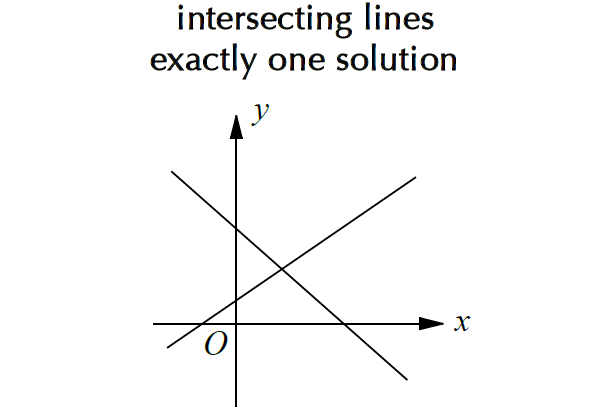
Write both the linear equations in slope intercept form, that is
y = mx + b
where m is the slope and b is the y-intercept.
If two lines have different slopes (y-intercepts may be same or different), then the system has one solution.
Example :
y = 3x + 4
y = -5x + 2
Linear System with Infinitely Many Solutions
If the two lines coincide (touching each other in all the points), then the system has infinitely many solutions.
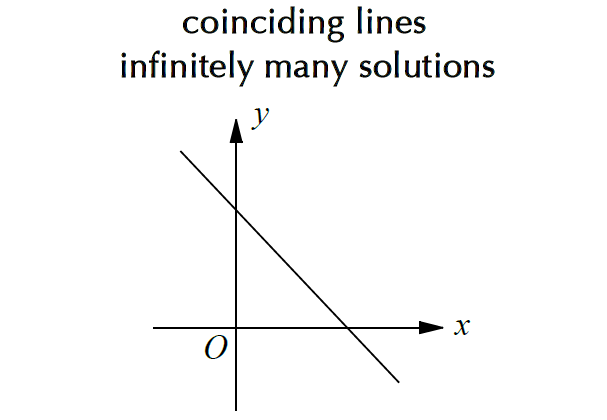
Write both the linear equations in slope intercept form. If two lines have same slope and same y-intercept, then the system has infinitely many solutions.
Example :
y = -2x + 3
y = -2x + 3
Linear System with No Solution
If the two lines are parallel, then will never intersect and the system has no solution
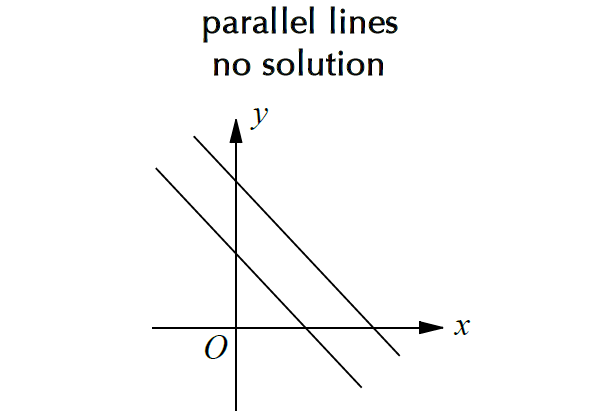
Write both the linear equations in slope intercept form. If two lines have same slope and different y-intercepts, then the system has no solution.
Example :
y = -3x + 4
y = -3x + 5
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 45)
Jan 18, 26 06:52 PM
10 Hard SAT Math Questions (Part - 45) -
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations
