SOLVING SYSTEMS OF LINEAR EQUATIONS BY GRAPHING WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
Solve the given system of equations by graphing.
x + y - 4 = 0
3x - y = 0
Problem 2 :
Solve the given system of equations by graphing.
3x - y - 3 = 0
x - y - 3 = 0
Problem 3 :
Lily and her friends visit the concession stand at a football game. $2 is charged for a sandwich and $1 is charged for a lemonade by the stand. The friends buy a total of 8 items for $11. Say how many sandwiches and how many lemonades they bought.

Answers
1. Answer :
x + y - 4 = 0
3x - y = 0
Step 1 :
Let us re-write the given equations in slope-intercept form (y = mx + b).
y = - x + 4
(slope is -1 and y-intercept is 4)
y = 3x
(slope is 3 and y-intercept is 0)
Based on slope and y-intercept, we can graph the given equations.
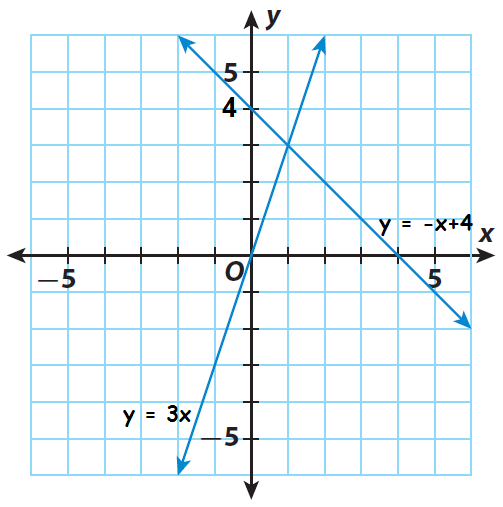
Step 2 :
Find the point of intersection of the two lines. It appears to be (1, 3). Substitute to check if it is a solution of both equations.
x + y - 4 = 0
1 + 3 - 4 = 0 ?
4 - 4 = 0 ?
0 = 0 True
3x - y = 0
3(1) - 3 = 0 ?
3 - 3 = 0 ?
0 = 0 True
Because the point (1, 3) satisfies both the equations, the solution of the system is (1, 3).
2. Answer :
3x - y - 3 = 0
x - y - 3 = 0
Step 1 :
Let us re-write the given equations in slope-intercept form.
y = 3x - 3
(slope is 3 and y-intercept is -3)
y = x - 3
(slope is 1 and y-intercept is -3)
Based on slope and y-intercept, we can graph the given equations.
Step 2 :
Find the point of intersection of the two lines. It appears to be (0, -3). Substitute to check if it is a solution of both equations.
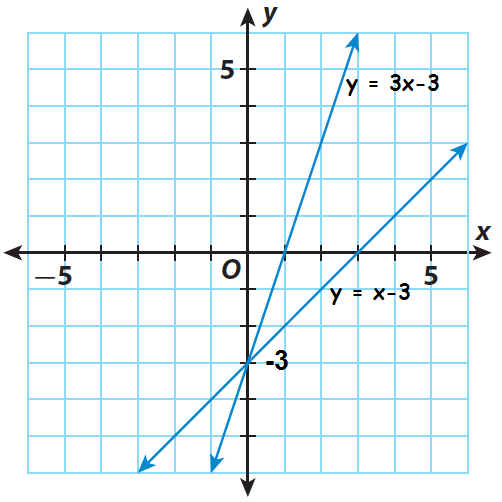
3x - y - 3 = 0
3(0) - (-3) - 3 = 0 ?
0 + 3 - 3 = 0 ?
0 = 0 True
x - y - 3 = 0
0 - (-3) - 3 = 0 ?
3 - 3 = 0 ?
0 = 0 True
Because the point (0, -3) satisfies both the equations, the solution of the system is (0, -3).
3. Answer :
Step 1 :
Let "x" be the no. of sandwiches and "y" be the no. of lemonades.
No. of sandwiches + No. of lemonades = Total items
x + y = 8 -------- (1)
Step 2 :
Write an equation which represents the money spent on the items.
Cost of "x" no. of sandwiches = 2x
Cost of "y" no. of sandwiches = 1y
Total cost = $11
Then, we have
2x + 1y = 11 -------- (2)
Step 3 :
Write the equations (1) and (2) in slope-intercept form. Then graph.
(1) ----- > x + y = 8 ----- > y = -x + 8
(2) ---- > 2x + 1y = 11 --- > y = -2x + 11
Graph the equations y = -x + 8 and y = -2x + 11.
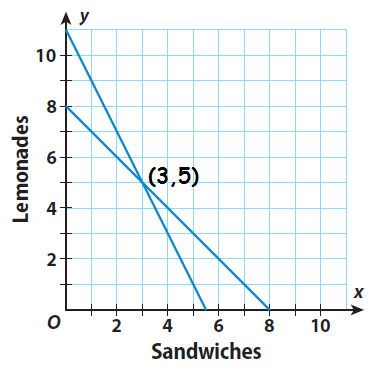
Step 4 :
Look at the graph and identify the solution of the system of equations. Check your answer by substituting the ordered pair into both equations.
The point of intersection of the lines is (3, 5).
Let us check whether the ordered pair (3, 5) satisfies both the equations.
y = -x + 8
5 = -3 + 8
5 = 5
y = -2x + 11
5 = -2(3) + 11
5 = -6 + 11
5 = 5
Since the ordered pair (3, 5) satisfies both the equations, the solution of the system is (3, 5).
Step 5 :
Interpret the solution in the original context.
Lily and her friends bought 3 sandwiches and 5 lemonades.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 06, 26 04:54 AM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4) -
10 Hard SAT Math Questions (Part - 3)
Jan 05, 26 06:34 PM
10 Hard SAT Math Questions (Part - 3)

