SOLVING SYSTEMS OF EQUATIONS USING INVERSE MATRICES

This method can be applied only when the coefficient matrix is a square matrix and non-singular. Consider the matrix equation AX = B ,

Pre-multiplying both sides of (1) by A⁻¹, we get

A⁻¹(AX)  =  A⁻¹B

(A⁻¹A) X  =  A⁻¹B

IX  =  A⁻¹B

X  =  A⁻¹B

Solved Questions

Question 1 :

Solve the following system of linear equations by matrix inversion method:

(i) 2x + 5y = −2, x + 2y = −3

Solution :

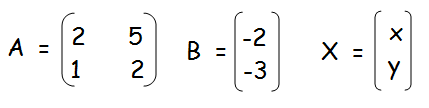
X = A^-1 B

A^-1  =  (1/|A|) adj A

|A|  = 4 - 5  =  -1

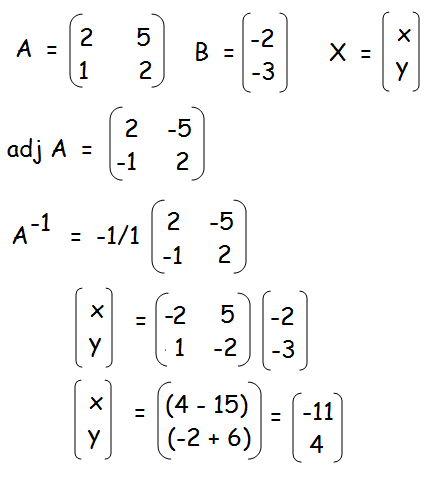
Hence the value of x and y are -11 and 4 respectively.

Question 2 :

(ii) 2x − y = 8, 3x + 2y = −2

Solution :

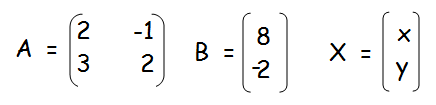
X = A^-1 B

A^-1  =  (1/|A|) adj A

|A|  = 4 + 3  =  7

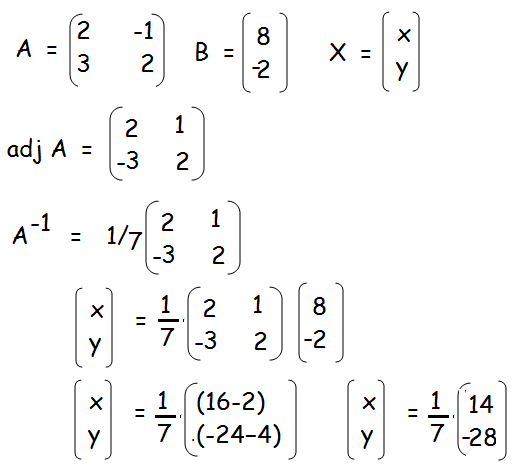
x  =  14/7  =  2

y  =  -28/7  =  -4

Hence the values of x and y are 2 and -4 respectively.

Question 3 :

(iii) 2x + 3y − z = 9, x + y + z = 9, 3x − y − z = −1

Solution :

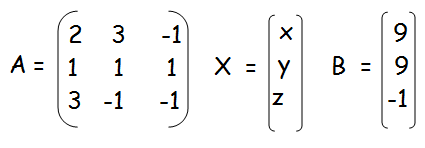
|A|  =  2(-1 + 1) - 3(-1 - 3) - 1(-1 -3)

  =  2(0) - 3(-4) - 1(-4)

  =  12 + 4

|A|  =  16

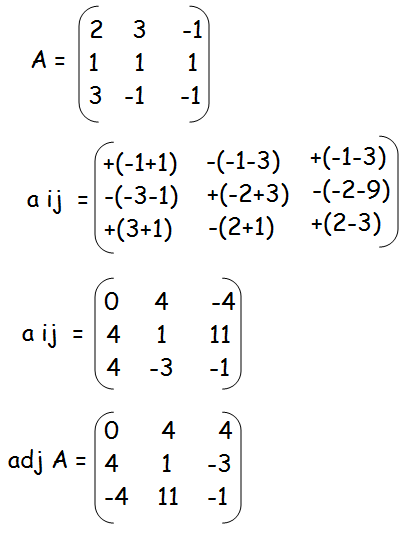
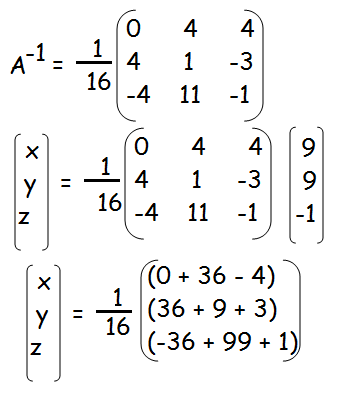
x = 32/16  =  2

y = 48/16  =  3

z  =  64/16  =  4

Hence the values of x, y and z are 2, 3 and 4 respectively. 

Question 4 :

(iv) x + y + z − 2 = 0, 6x − 4y + 5z − 31 = 0, 5x + 2y + 2z =13

Solution :

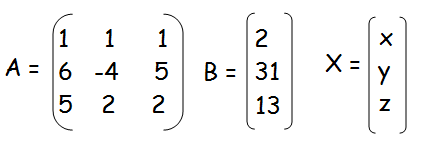
|A|  =  1(-8 - 10) - 1(12 - 25) + 1(12 + 20)

  =  1(-18) - 1(-13) + 1(32)

  =  -18 + 13 + 32

  =  27

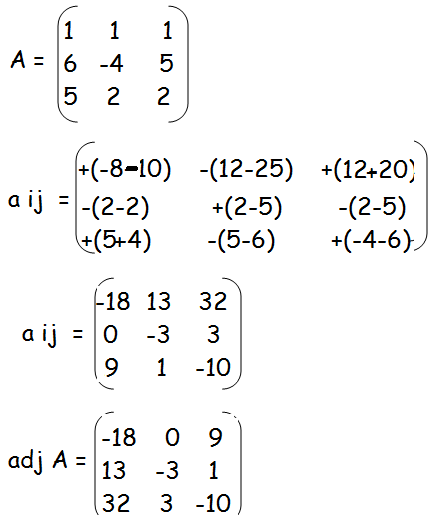
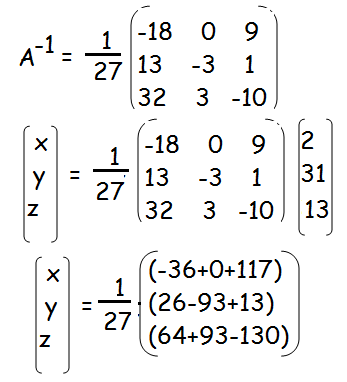
x = 81/27  =  3

y  =  -54/27  =  -2

z  =  27/27  =  1

Hence the values of x, y and z are 3, -2 and 1 respectively.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.