SOLVING SYSTEMS OF EQUATIONS GRAPHICALLY WORKSHEET

Problem 1 : 

Solve the following system of equations by graphically. 

x + y - 4  =  0 

3x - y  =  0

Problem 2 : 

Solve the following system of equations by graphically. 

3x - y - 3  =  0 

x - y - 3  =  0

Solutions

Problem 1 : 

Solve the following system of equations by graphically. 

x + y - 4  =  0 

3x - y  =  0

Solution :

Step 1 :

Let us re-write the given equations in slope-intercept form  (y = mx + b). 

y  =  - x + 4

(slope is -1 and y-intercept is 4) 

y  =  3x 

(slope is 3 and y-intercept is 0) 

Based on slope and y-intercept, we can graph the given equations. 

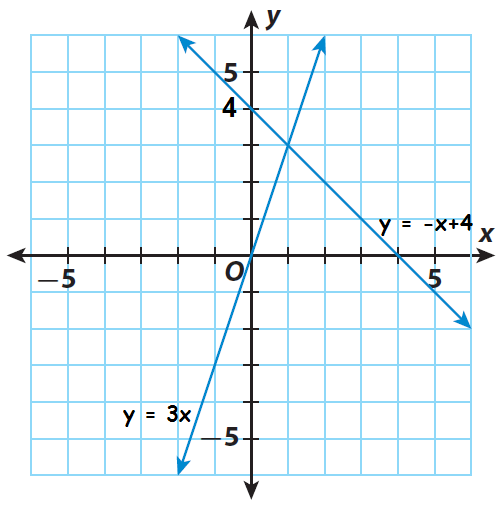
Step 2 :

Find the point of intersection of the two lines. It appears to be (1, 3). Substitute to check if it is a solution of both equations.

Because the point (1, 3) satisfies both the equations, the solution of the system is (1, 3).  

Problem 2 : 

Solve the following system of equations by graphically. 

3x - y - 3  =  0 

x - y - 3  =  0

Solution :

Step 1 :

Let us re-write the given equations in slope-intercept form. 

y  =  3x - 3

(slope is 3 and y-intercept is -3) 

y  =  x - 3 

(slope is 1 and y-intercept is -3) 

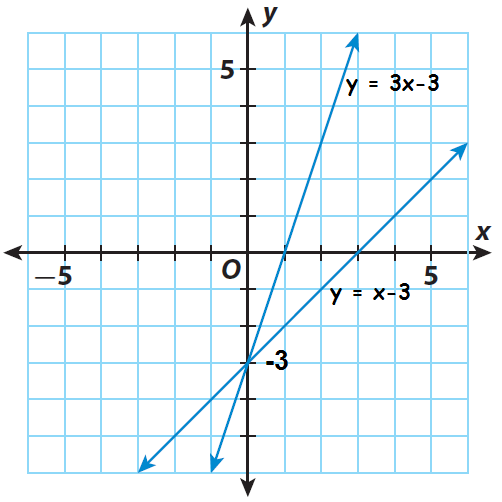
Based on slope and y-intercept, we can graph the given equations. 

Step 2 :

Find the point of intersection of the two lines. It appears to be (0, -3). Substitute to check if it is a solution of both equations.

Because the point (0, -3) satisfies both the equations, the solution of the system is (0, -3).  

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.