SOLVING SYSTEMS BY SUBSTITUTION

The method of substitution can be used to solve systems of linear equations by solving an equation for one variable and then substituting the resulting expression for that variable into the other equation.

The following steps will be useful to solve system of equations by substitution. 

Step 1 :

Solve one of the equations for one of its variables.

Step 2 :

Substitute the expression from step 1 into the other equation and solve for the other variable.

Step 3 :

Substitute the value from step 2 into either original equation and solve to find the value of the variable in step 1.

Solved Examples

Example 1 :

Solve the system of linear equations by substitution. Check your answer by graphing.

4x + y  =  8

-3x + y  =  1

Solution : 

Step 1 :

Solve an equation for one variable.

Select one of the equation, say -3x + y  =  1.

Solve for the variable y in terms of x. 

Add 3x on both sides. 

(-3x + y) + 3x  =  (1) + 3x

-3x + y + 3x  =  1 + 3x

Simplify. 

y  =  1 + 3x

Step 2 : 

Substitute the expression for y in the other equation and solve.

4x + y  =  8

4x + (1 + 3x)  =  8

Combine like terms. 

7x + 1  =  8

Subtract 1 from both sides.

7x  =  7

Divide both sides by 7. 

7x / 7  =  7 / 7

x  =  1

Step 3 : 

Substitute the value of x we got above (x = 1) into one of the equations and solve for the other variable, y.

4x + y  =  8

4(1) + y  =  8

4 + y  =  8

Subtract 4 from both sides.

y  =  8

Hence, the solution of the system is (1, 8).

Step 4 : 

Check the solution by graphing. 

To graph the equations, write them in slope-intercept form.

That is, 

y  =  mx + b  

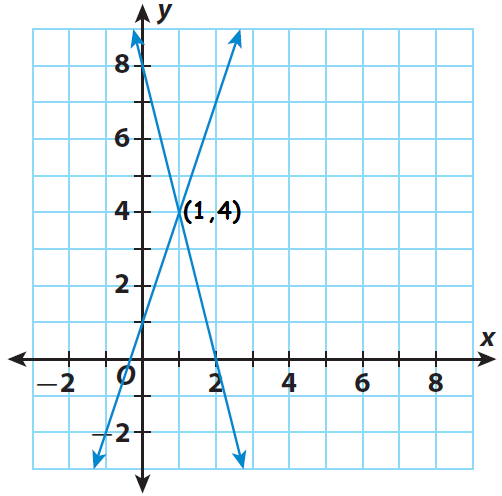
The point of intersection is (1, 4).

Example 2 :

Solve the system of linear equations by substitution. Check your answer by graphing.

x + y  =  8

2x + y  =  11

Solution : 

Step 1 :

Solve an equation for one variable.

Select one of the equation, say x + y  =  8.

Solve for the variable y in terms of x. 

Subtract x from both sides. 

(x + y) - x  =  (8) - x

x + y - x  =  8 - x

Simplify. 

y  =  8 - x

Step 2 : 

Substitute the expression for y in the other equation and solve.

2x + y  =  11

2x + (8 - x)  =  11

Combine like terms. 

x + 8  =  11

Subtract 8 from both sides.

x  =  3

Step 3 : 

Substitute the value of x we got above (x = 3) into one of the equations and solve for the other variable, y.

x + y  =  8

3 + y  =  8

Subtract 3 from both sides.

y  =  5

Hence, the solution of the system is (3, 5).

Step 4 : 

Check the solution by graphing. 

To graph the equations, write them in slope-intercept form.

That is, 

y  =  mx + b  

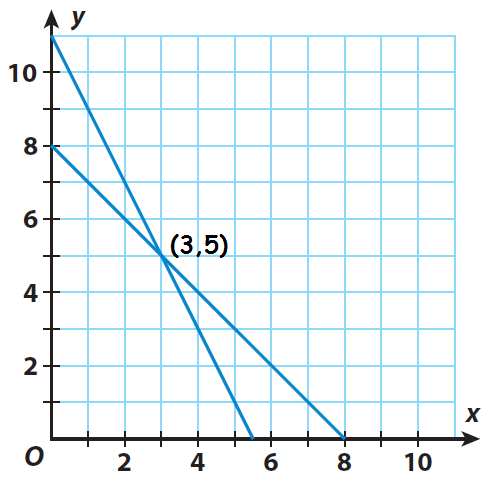
The point of intersection is (1, 4).

Example 3 :

A park charges $10 for adults and $5 for kids. How many many adults tickets and kids tickets were sold, if a total of 548 tickets were sold for a total of $3750 ? 

Solution : 

Step 1 :

Let "x" be the number of adults tickets and "y" be the number of kids tickets.

No. of adults tickets + No. of kids tickets  =  Total

x + y  =  548 -----(2)

Step 2 : 

Write an equation which represents the total cost.

Cost of "x" no. adults tickets  =  10x

Cost of "y" no. of kids tickets  =  5y

Total cost  =  $3750

Then, we have 

10x + 5y  =  3750

 Divide both sides by 5.

2x + y  =  750 -----(2)

Step 3 :

Solve an equation for one variable.

Select one of the equation, say x + y  =  548.

Solve for the variable y in terms of x. 

Subtract x from both sides. 

(x + y) - x  =  (548) - x

y  =  548 - x

Step 4 : 

Substitute the expression for y in the other equation and solve.

2x + y  =  750

2x + (548 - x)  =  750

Combine like terms. 

x + 548  =  750

Subtract 548 from both sides.

x  =  202

Step 5 : 

Substitute the value of x we got above (x = 202) into one of the equations and solve for the other variable, y.

x + y  =  548

202 + y  =  548

Subtract 202 from both sides.

y  =  346

So, the solution of the system is (202, 346).

Step 6 : 

Interpret the solution in the original context.

So, the number of adults tickets sold is 202 and the number of kids tickets sold is 346.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.