SOLVING SYSTEMS BY ELIMINATION

Example 1 :

Solve the system of equations using elimination method. Check the solution by graphing.

2x - 3y  =  12

x + 3y  =  6

Solution :

2x - 3y  =  12 -----(1)

x + 3y  =  6 -----(2)

In the given two equations, the variable y is having the same coefficient. And also, the variable y is having different signs.

So we can eliminate the variable y by adding the two equations. 

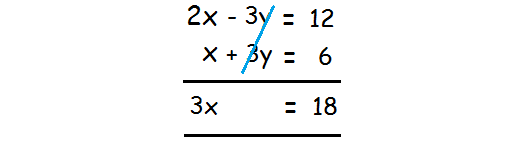
Divide both sides by 3.

x = 6

Substitute 6 for x in (2).

(2)----> 6 + 3y = 6

Subtract 6 from each side.

3y = 0

Divide each side by 3.

y = 0

Write the solution as ordered pair.

(x, y) = (6, 0)

Check the solution by graphing. 

To graph the equations, write them in slope-intercept form y = mx + b.

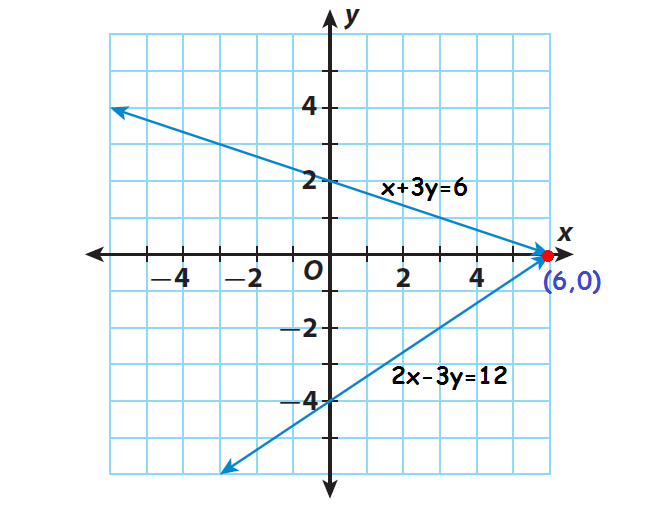
The point of intersection is (6, 0).

Example 2 :

Sum of the cost price of two products is $50. Sum of the selling price of the same two products is $52. If one is sold at 20% profit and other one is sold at 20% loss, find the cost price of each product.

Solution :

Let 'x' and 'y' be the cost prices of two products. 

x + y = 50 ----(1)

Let us assume that x is sold at 20% profit.

Then, the selling price of x :

= 120% of x

= 1.2x

Let us assume that y is sold at 20% loss.

Then, the selling price of y :

= 80% of 'y'

= 0.8y

Given : Selling price of x + selling price of y = 52.

1.2x + 0.8y = 52

Multiply both sides by 10.

12x + 8y = 520

Divide each side by 4.

3x + 2y = 130 ----(2)

Solve (1) and (2).

(2) - (1) ⋅ 2 : 

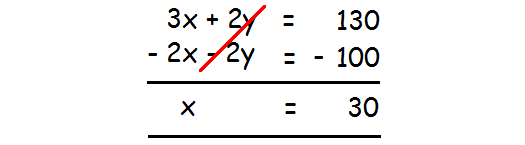
Substitute 30 for x in (1). 

30 + y = 50

Subtract 30 from each side.

y = 20

So, the cost prices of two products are $30 and $20.

Example 3 :

The sum of two numbers is 22. The difference is 6. What are the two numbers?

Solution :

Let x and y be the two numbers.

sum of two numbers = 22

x + y = 22 -----(1)

Difference of two numbers = 6

x - y = 6 -----(2)

(1) + (2)

2x = 28

x = 28/2

x = 14

Applying x = 14 in (1), we get

14 + y = 22

y = 22 - 14

y = 8

So, the required numbers are 14 and 8.

Example 4 :

You and your friend are making 30 liters of sodium water. You have liters of 10% sodium and your friend has liters of 22% sodium. How many of your liters and how many of your friend's liters should you mix to make 30 liters of 15% sodium?

Solution :

Quantity of water i have = x 

Quantity of water my friend has = y

x + y = 30 -----(1)

10% of x + 22% of y = 15% of (x  y)

0.1x + 0.22y = 0.15(x + y)

0.1x + 0.22y = 0.15x + 0.15y

0.1x - 0.15x + 0.22y - 0.15y = 0

-0.05x + 0.07y = 0 -----(2)

(1) 0.05 ==> 0.05x + 0.05y = 1.5

(1) + (2)

0.07y + 0.05y = 0 + 1.5

0.12y = 1.5

y = 1.5 / 0.12

y = 12.5

Applying the value of y in (1), we get 

x + 12.5 = 30

x = 30 - 12.5

x = 17.5

So, quantity of water i have is 17.5 liter and quantity of water my friend has is 12.5 liter.

Example 5 :

Solve the system of equations by elimination method.

2(x - 2y) = 26 - 5y

3(y - x) = 2(y - 7)

Solution :

2(x - 2y) = 26 - 5y

Distributing 2, 

2x - 4y = 26 - 5y

2x - 4y + 5y = 26

2x + y = 26 -----(1)

3(y - x) = 2(y - 7)

Distributing 3, we get 

3y - 3x = 2y - 14

3y - 2y - 3x = -14

-3x + y = 14 ------(2)

(1) - (2)

2x - (-3x) = 26 - 14

2x + 3x = 26 + 14

5x = 40

x = 40/5

x = 8

Applying x = 8 in (1), we get

2(8) + y = 26

16 + y = 26

y = 26 - 16

y = 10

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.