SOLVING SYSTEMS BY ELIMINATION WITH MULTIPLICATION

Problem 1 :

Solve the system of equations by multiplying and adding.

3x - 5y  =  -17

2x + 15y  =  7

Solution :

Step 1 :

Let us eliminate the variable y in the given two equations. 

3x - 5y  =  -17 -------- (1)

2x + 15y  =  7 -------- (2)

Step 2 :

To make the coefficient of y same in both the equations, multiply the first equation by 3.  

(1) ⋅ 3 ----- > 9x - 15y  =  -51 -------- (3)

In equations (2) and (3), the variable y is having the same coefficient, but having different signs.

Step 3 :

Add the equations (2) and (3) to eliminate the variable y. 

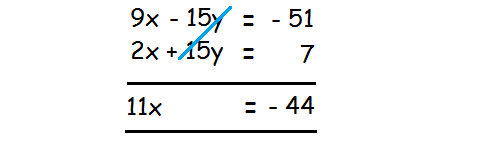
Divide both sides by 11.

11x / 11  =  - 44 / 11

x  =  - 4

Step 4 : 

Substitute the value of x into one of the equations to find the value of y. 

3x - 5y  =  -17

3(-4) - 5y  =  -17

-12 - 5y  =  -17

Add 12 to both sides.

(-12 - 5y) + 12  =  (-17) + 12

-12 - 5y + 12  =  -17 + 12

Simplify.

-5y  =  -5

Divide both sides by -5

-5y / (-5)  =  -5 / (-5)

y  =  1

Hence, the solution to the system is

(x, y)  =  (-4, 1)

Problem 2 :

Contestants in the Run-and-Bike-a-thon run for a specified length of time, then bike for a specified length of time. Jacob ran at an average speed of 5.2 mi/h and biked at an average speed of 20.6 mi/h, going a total of 14.2 miles. Alex ran at an average speed of 10.4 mi/h and biked at an average speed of 18.4 mi/h, going a total of 17 miles. For how long do contestants run and for how long do they bike ?

Solution :

Step 1 :

Let the contestants run "x" hours and bike "y" hours.

Using the formula, Distance  =  Speed x Time, 

Jacob :  5.2x + 20.6y  =  14.2  

Alex :  10.4x + 18.4y  =  17

Step 2 :

In both the equations we have decimal. In the terms we have decimal, the maximum number of digits after the decimal is 1. 

So multiply both the equations by 10.

10(5.2x + 20.6y)  =  10(14.2)  

52x + 206y  =  142 -------- (1)

10(10.4x + 18.4y)10  =  10(17)

104x + 184y  =  170 -------- (2)

Step 3 : 

Eliminate one of the variables to get the value of the other variable.

In (1) and (2), both the variables "x" and "y" are not having the same coefficient.

One of the variables must have the same coefficient. 

So multiply both sides of (1) by 2 to make the coefficients of "x" same in both the equations.  

(1) ⋅ 2 -------->  104x + 412y  =  284 ----------(3) 

Variable "x" is having the same sign in both (1) and (2). 

To change the sign of "x" in (3), multiply both sides of (2) by negative sign.

- (104x + 412y)  =  - 284

- 104x - 412y  =  - 284 --------(4)

Step 4 : 

Add the equations (2) and (4) to eliminate the variable y. 

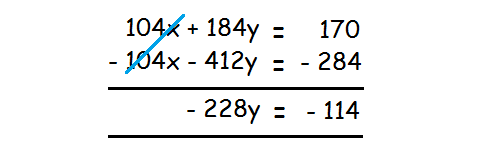
Divide both sides by -228.

-228y / (-228)  =  - 114 / (-228)

y  =  0.5

Step 5 : 

Plug y  =  0.5 in (1) to get the value of x. 

             (1) --------> 52x + 206(0.5)  =  142

52x + 103  =  142

Subtract 103 from both sides. 

52x  =  39

Divide both sides by 52.

52x / 52  =  39 / 52

x  =  0.75

So, the contestants run 0.75 hour and bike 0.5 hour.

Problem 3 :

A business with two locations buys seven large delivery vans and five small delivery vans. Location A receives five large vans and two small vans for a total cost of $235,000. Location B receives two large vans and three small vans for a total cost of $160,000. What is the cost of each type of van?

Solution :

Let x be the cost of large vans and y be the cost of small vans.

Location A :

5x + 2y = 235000 --------(1)

Location B :

2x + 3y = 160000 --------(2)

(1) ⋅ 3 - (2) ⋅ 2

15x + 6y - (4x + 6y) = 705000 - 320000

15x + 6y - 4x - 6y = 385000

11x = 385000

x = 35000

Applying the value of x, we get

5(35000) + 2y = 235000

175000 + 2y = 235000

2y = 235000 - 175000

2y = 60000

y = 30000

So, cost of large vans is 35000 and cost of small vans is 30000.

Problem 4 :

A music website charges x dollars for individual songs and y dollars for entire albums.

Person A pays $25.92 to download 6 individual songs and 2 albums.

Person B pays $33.93 to download 4 individual songs and 3 albums.

Write a system of linear equations that represents this situation. How much does the website charge to download a song? an entire album?

Solution :

Let x be the cost of individual songs and y be the cost of albums.

6x + 2y = 25.92  --------(1)

4x + 3y = 33.93   --------(2)

(1) ⋅ 3 - (2) ⋅ 2

18x + 6y - (8x + 6y) = 77.76 - 67.86

18x + 6y - 8x - 6y = 9.9

x = 9.9/10

x = 0.99

Applying the value of x, we get

6(0.99) + 2y = 25.92

5.94 + 2y = 25.92

2y = 25.92 - 5.94

2y = 19.98

y = 9.99

Cost of individual song is $0.99 cost of album is $9.99.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.