SOLVING SYSTEM OF LINEAR EQUATIONS USING RANK METHOD

Write down the given system of equations in the form of a matrix equation AX = B.

Step 1 :

Find the augmented matrix [A, B] of the system of equations.

Step 2 :

Find the rank of A and rank of [A, B] by applying only elementary row operations.

Note :

Column operations should not be applied.

Step 3 :

Problem :

Test for consistency and if possible, solve the following systems of equations by rank method.

(i) x − y + 2z = 2, 2x + y + 4z = 7, 4x − y + z = 4

Solution :

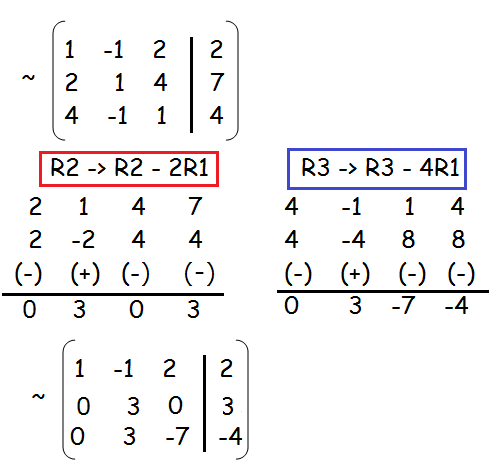
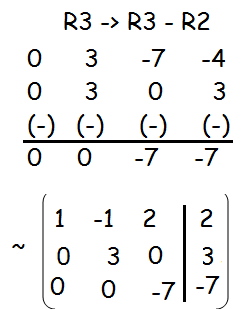
 ρ (A) = ρ ([A| B]) = 3

Since  ρ (A) and ρ ([A| B]) are equal, it has unique solution.

x - y + 2z  =  2 ------(1)

3y  =  3

-7z  =  -7

z  =  1

y  =  1

By applying the values of y and z in (1), we get

x - 1 + 2(1)  =  2

x - 1 + 2  =  2

 x  =  1

Hence the solution is (1, 1, 1)

(ii) 3x + y + z = 2, x − 3y + 2z =1, 7x − y + 4z = 5

Solution :

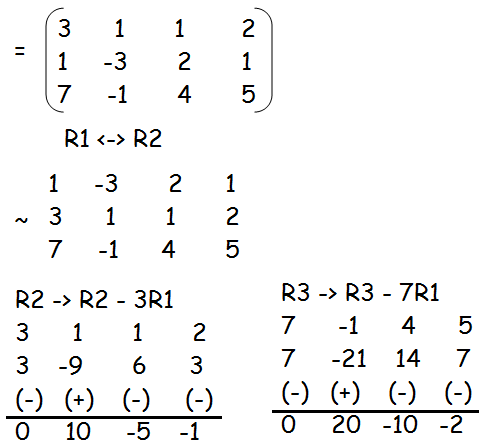
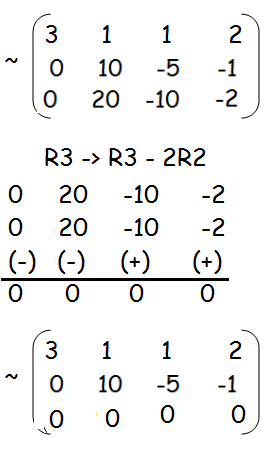
 ρ (A) = ρ ([A| B]) = 2

Since  ρ (A) and ρ ([A| B]) are equal and it is less than 3, it has infinitely many solution.

3x + y + z  =  2 ------(1)

10y - 5z  =  -1

z = t

10y  =  5z

10y  =  5t 

y  =  t/2

By applying the values of y and z, we get

3x + (t/2) + t  =  2

3x  =  2 - t - (t/2)

  3x  =  2 - (3t/2)

  3x  =  (4 - 3t)/2

x  =  (4 - 3t) /6

Hence the solutions are ((4 - 3t)/6, t/2, t) , where t ∈ R.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.