SOLVING SYSTEM OF EQUATIONS BY GRAPHING

Solve each system by graphing.

Example 1 :

x + y = 7; x - y = 3

Solution :

x + y = 7 -----(1) 

x − y = 3 -----(2)

From (1),

y  =  7 - x

Substitute some random values for x and solve for y. 

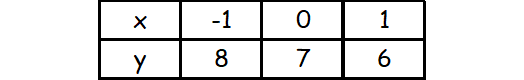
The points on the first line are

(-1, 8), (0, 7), (1, 6)

From (2),

y  =  x - 3

Substitute some random values for x and solve for y. 

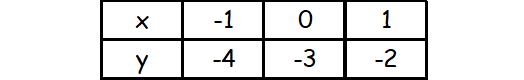
The points on the second line are

(-1, -4), (0, -3), (1, -2)

Plot the points from the above tables and sketch the graph. 

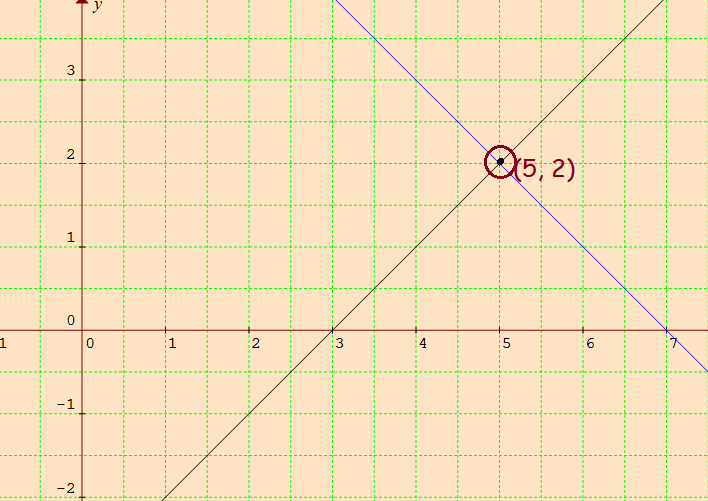
The point of intersection of the two lines is the solution.

So, the solution is (x, y) = (5, 2).

Example 2 :

3x + 2y = 4; 9x + 6y - 12 = 0

Solution :

3x + 2y = 4 -----(1)

9x + 6y = 12 -----(2)

From (1),

2y  =  -3x + 4

y  =  (-3x + 4)/2

y  =  -3x/2 + 4/2

y  =  -3x/2 + 2

From (2),

6y  =  -9x + 12

y  =  (-9x + 12)/6

y  =  -9x/6 + 12/6

y  =  -3x/2 + 2

Because both the lines are same, it has infinitely many solution.

Example 3 :

(x/2) + (y/4) = 1

(x/2) + (y/4) = 2

Solution :

Because the coefficients of x and y are same, they are parallel lines and they never intersect. So, there is no solution. 

Example 4 :

x - y = 0; y + 3 = 0

Solution :

x - y = 0 -----(1)

y + 3 = 0 -----(2)

From (1),

-y  =  -x

y  =  x

Substitute some random values for x and solve for y. 

The points on the first line are

(-1, -1), (0, 0), (1, 1)

From (2), 

y  =  -3

Plot the points from the above table and sketch the graph. 

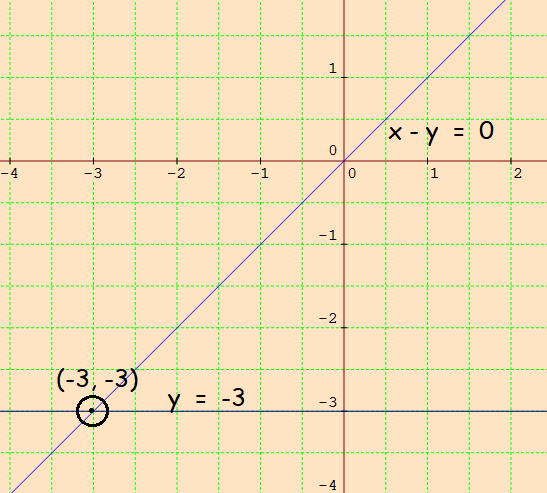
Two lines intersect at (-3, -3). 

So, the solution is (x, y) = (-3, -3).

Example 5 :

  y = 2x + 1; y + 3x - 6 = 0

Solution :

y = 2x + 1 -----(1)

y + 3x = 6 -----(2)

From (1),

y  =  2x + 1

Substitute some random values for x and solve for y. 

The point on the first line are

(-1, -1) (0, 1), (1, 3)

From (2),

y + 3x  =  6

 y  =  -3x + 6

Substitute some random values for x and solve for y. 

The point on the first line are

(-1, 9) (0, 6), (1, 3)

Plot the points from the above tables and sketch the graph. 

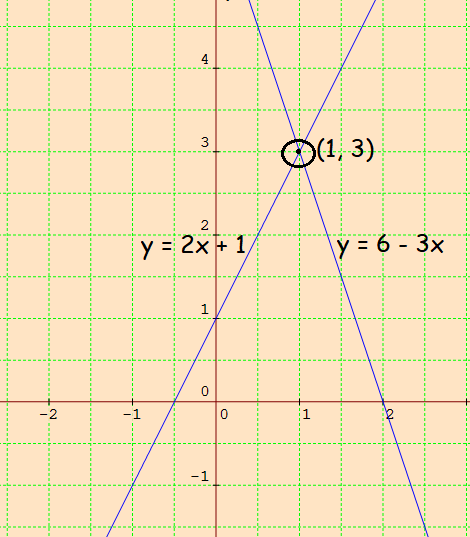
Two lines intersect at (1, 3). 

So, the solution is (x, y) = (1, 3).

Example 6 :

x = -3 ; y = 3

Solution :

Sketch the graph of x = -3 and y = 3.  

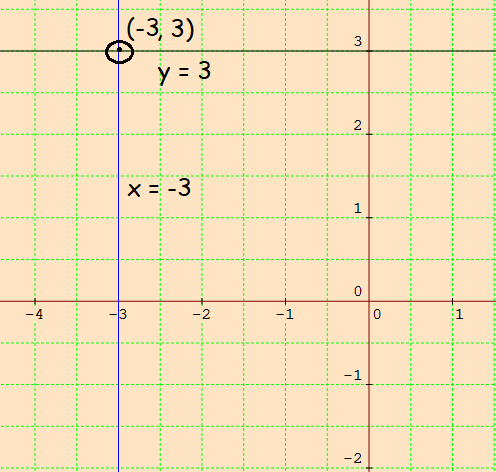
The two lines intersect at (-3, 3). 

So, the solution is (-3, 3). 

Example 7 :

Two cars are 100 miles apart. If they drive towards each other they will meet in 1 hour. If they drive in the same direction they will meet in 2 hours. Find their speed by using graphical method.

Solution :

Let x and y be the speeds of the cars in miles per hour. 

Given : Cars are 100 miles apart. If they drive towards each other, they will meet in 1 hour.

x + y  =  100

y  =  -x + 100 -----(1)

Substitute some random values for x and solve for y. 

Given :  If they drive in the same direction they will meet in 2 hours. 

Distance  =  Speed x Time

Distance covered by the cars in two hours :

2x miles, 2y miles

They meet after 2 hours.

2x  =  2y + 100

x  =  y + 50

y  =  x - 50 -----(2)

Substitute some random values for x and solve for y. 

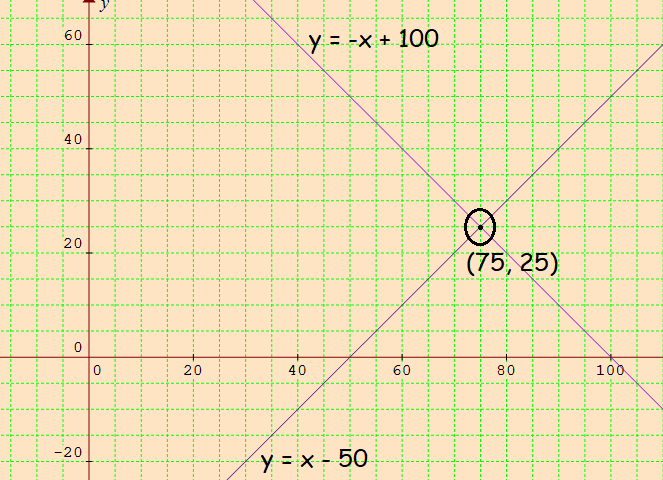
The two lines intersect at (75. 25). 

(x, y)  =  (75, 25)

Speeds of the cars are 75 miles per hour and 25 miles per hour. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.