SOLVING SPECIAL SYSTEMS BY GRAPHING

We may know to solve system of linear equations using the methods like substitution or elimination.

In this section, we are going to see, how to solve the system of linear equations by graphing. 

To solve the system of linear equations by graphing, we have to sketch the graph of each equation. 

The point at which the graphs of the linear equations (straight lines) intersect is the solution of the given system of equations.

The x and y coordinates in the point of intersection are the values of x and y respectively. 

For example, if(a, b) is the point of intersection, 'a' is the value of x and 'b' is the value of y. 

That is. 

x  =  a

y  =  b

Special Systems

The following are special systems of linear equations. 

1. If the graphs (straight lines) of the linear equations interest at only one point, then the system will have only one solution.    

2. If the graphs (straight lines) of the linear equations are parallel, then the lines will never interest and there will be no solution to the system. 

3. 2. If the graphs (straight lines) of the linear equations represents the same line, all ordered pairs on the line will make both equations true and all points on the line are points of intersection.

So, the system has infinitely many solutions.

Examples

Example 1 :

Solve the given system of equations by graphing. 

x + y  =  7 

4x + 4y  =  12

Solution :

Step 1 :

Write the given equations in slope-intercept form.

y = mx + b 

x + y  =  7 

y  =  - x + 7

(slope is -1 and y-intercept is 7) 

4x + 4y  =  12

Divide both sides by 4.

x + y  =  3

y  =  - x + 3

(slope is -1 and y-intercept is 3) 

Based on slope and y-intercept, we can graph the given equations. 

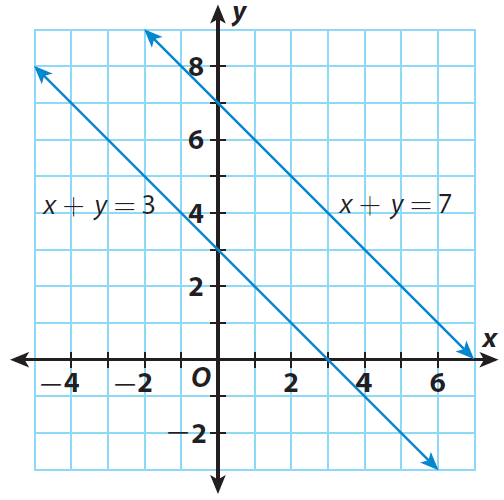
Step 2 :

In the above graph, the lines do not intersect. They appear to be parallel and and no points in common.

Does this linear system have a solution ? Use the graph to explain.

Because the lines are parallel and they do not intersect, there is no point of intersection. So, the system has no solution.  

Reflection : 

1. Can you conclude that the system of linear equation has no solution without graphing ?

Yes

We have to find the slopes and y-intercepts of the given two lines. If the slopes are equal, but y-intercepts are different, the lines will be parallel. Then, the system will not have solution. 

2. Can you conclude that the system of linear equation has infinitely many solutions without graphing ?

Yes

We have to find the slopes and y-intercepts of the given two lines. If the slopes are equal and y-intercepts are also equal, both the equations represent the same line. All ordered pairs on the line will make both equations true and all points on the line are points of intersection.

Then, the system will have infinitely many solutions.

Example 2 :

Determine whether the system given below has one solution, infinitely many solutions or no solution.  

x + y  =  3

2x + 2y  =  6 

Solution :

Step 1 :

Write the given equations in slope-intercept form.

y = mx + b 

x + y  =  3

y  =  - x + 3

(slope is -1 and y-intercept is 3) 

2x + 2y  =  6 

Divide both sides by 2.

x + y  =  3

y  =  - x + 3

(slope is -1 and y-intercept is 3) 

Step 2 :

The slopes of both the equations are same and y-intercepts are also same. 

So, both the equations represents the same line. All ordered pairs on the line will make both equations true and all points on the line are points of intersection.

So, the system has infinitely many solutions.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.