SOLVING QUADRATIC INEQUALITIES WORKSHEET FOR GRADE 11

Problem 1 :

Solve : 

2x² + x - 15 ≤ 0

Problem 2 : 

Solve : 

-x² + 3x - 2 ≥ 0

Detailed Answer Key

Problem 1 :

Solve : 

2x² + x - 15 ≤ 0

Solution :

First let us solve the given quadratic equation by factoring.

2x² + x − 15 = 0

2x² + 6x - 5x  − 15 = 0

2x(x + 3) - 5(x + 3) = 0

(2x - 5) (x + 3) = 0

2x - 5  =  0       x + 3  =  0

2x  =  5              x  =  -3

x  =  5/2

The critical numbers are -3 and 5/2. 

Now let us mark them in number line.

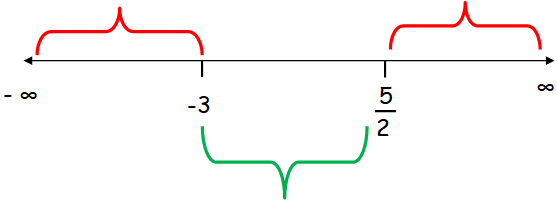
Applying any values within the interval, we get

From the above table, we come to know that the interval [-3, 5/2] satisfies the given inequality.

So, the solution is  [-3, 5/2].

Problem 2 : 

Solve : 

-x² + 3x - 2 ≥ 0

Solution :

First let us solve the given quadratic equation by factoring.

The coefficient of x must be positive, so we have to multiply the inequality by negative.

x² - 3x + 2 ≤ 0

Multiply the equation by negative.

x² - 3x + 2 = 0

x² - 1x - 2x + 2 = 0

x (x - 1) - 2(x - 1)  =  0

(x - 2) (x - 1)  =  0

x - 2  =  0             x - 1  =  0

x  =  2                   x  =  1

Writing them as intervals, we get

(-∞, 1] [1, 2] [2, ∞)

Applying any values within the interval, we get

From the above table, we come to know that the interval [1, 2] satisfies the given inequality.

So, the solution is  [1, 2].

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.