SOLVING QUADRATIC  INEQUALITIES ALGEBRAICALLY

Solving Factorable Quadratic Inequalities

Solving Non-Factorable Quadratic Inequalities

Solved Problems

Solve the following quadratic inequalities.

Example 1 :

x² + 5x + 6 ≥ 0

Solution :

x² + 5x + 6 ≥ 0

(x + 2)(x + 3) ≥ 0 ----(1)

Assume the above inequality as equation and solve for x.

(x + 2)(x + 3) = 0

x = -2  or   x = -3

Mark the two values -2 and -3 on the real number line and split up the real numbers into intervals as shown below.

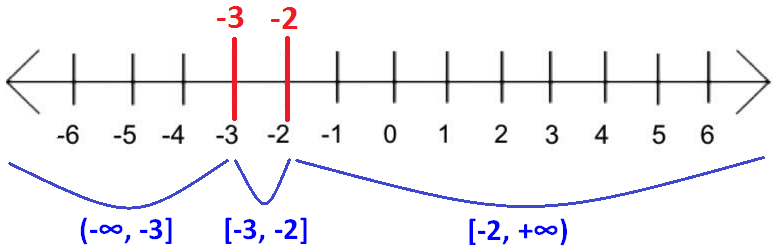
Testing the interval (-∞, -3] :

Take a random value in the interval (-∞, -3], say -4.

Substitute x = -4 into (1). 

(-4 + 2)(-4 + 3) ≥ 0

(-2)(-1) ≥ 0

2 ≥ 0 (TRUE)

The interval (-∞, -3] satisfies the given inequality.

Testing the interval [-3, -2] : 

Take a random value in the interval [-3, -2], say -2.5.

Substitute x = -2.5 for x into (1).

(-2.5 + 2)(-2.5 + 3) ≥ 0

(-0.5)(0.5) ≥ 0

-0.25 ≥ 0 (FALSE)

The interval [-3, -2] does not satisfy the given inequality.

Testing the interval [-2, +∞] : 

Take a random value in the interval [-2, +∞), say 0.

Substitute x = 0 into (1). 

(0 + 2)(0 + 3) ≥ 0

(2)(3) ≥ 0

6 ≥ 0 (TRUE)

The interval [-2, +∞) satisfies the given inequality.

Hence, the solution is

(-∞, -3] U [-2, +∞)

(or)

x ≤ -3  or  x ≥ -2

Example 2 :

-x² + 2x - 5 < 0

Solution :

-x² + 2x - 5 > 0

Multiply both sides by -1.

-1(-x² + 2x - 5) > -1(0)

x² - 2x + 5 > 0

The quadratic expression (x² - 2x + 5) is not factorable.

Write the corresponding quadratic function.

y = x² - 2x + 5

x² - 2x + 5 > 0 -----> y > 0 ----(1)

Find the value of the discriminant b² - 4ac.

b² - 4ac = (-2)² - 4(1)(5)

= 4 - 20

= -16 < 0

Since b² - 4ac < 0, the quadratioc function y = x² - 2x + 5  has no zeros, that is, the parabola represented by the above quadratic function does not intersect x-axis. And also, the leading coefficient of the quadratic function is 1. So the parabola opens up.

Since the parabola opens up and it does not intersect x-axis, the parabola is above the x-axis. So, the y-coordinates in all the points on the parabola will be greater than zero and and x-coordinate can be any real number.

Therefore, (1) is true and the solution for the given quadratic inequality is all real numbers, that is x ∈ R.  

Example 3 :

-x² + 4 ≥ 0

Solution :

-x² + 4 ≥ 0

Multiply both sides by -1.

-1(-x² + 4) ≤ -1(0)

x² - 4 ≤ 0

x² - 2² ≤ 0

(x + 2)(x - 2) ≤ 0 ----(1)

Assume the above inequality as equation and solve for x.

(x + 2)(x - 2) = 0

x = -2  or  x = 2

Mark the two values -2 and 2 on the real number line and split up the real numbers into intervals as shown below.

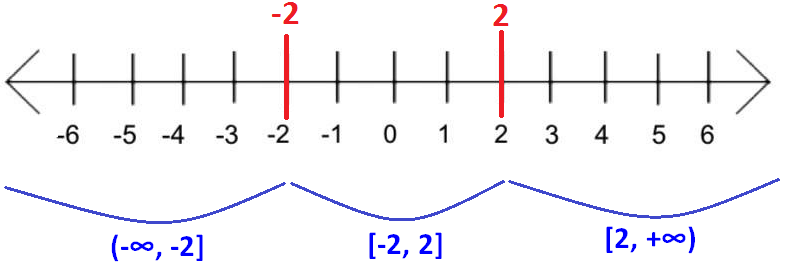
Testing the interval (-∞, -2] : 

Take a random value in the interval (-∞, -2], say -3.

Substitute x = -3 into (1).   

(-3 + 2)(-3 - 2) ≤ 0

(-1)(-5) ≤ 0

5 ≤ 0 (FALSE)

The interval (-∞, -2] does not satisfy the given inequality.

Testing the interval [-2, 2] : 

Take a random value in the interval [-2, 2], say 0.

Substitute x = 0 into (1).

(0 + 2)(0 - 2) ≤ 0

(2)(-2) ≤ 0

-4 ≤ 0 (TRUE)

The interval [-2, 2] satisfies the given inequality.

Testing the interval [2, +∞] : 

Take a random value in the interval [2, +∞), say 3.

Substitute x = 3 into (1).

(3 + 2)(3 - 2) ≤ 0

(5)(1) ≤ 0

5 ≤ 0 (FALSE)

The interval [2, +∞) does not satisfy the given inequality.

Hence the solution is

[-2, 2]

(or)

-2 ≤ x ≤ 2

Example 4 :

Solve the quadratic inequality given.

x² + 4x +7 < 0

Solution :

x² + 4x +7 < 0

The quadratic expression (x² + 4x +7) is not factorable.

Write the corresponding quadratic function.

y = x² + 4x +7

x² + 4x +7 < 0 -----> y < 0 ----(1)

Find the value of the discriminant b² - 4ac.

b² - 4ac = 4² - 4(1)(7)

= 16 - 28

= -12 < 0

Since b² - 4ac < 0, the quadratioc function y = x² - 2x + 5  has no zeros, that is, the parabola represented by the above quadratic function does not intersect x-axis. And also, the leading coefficient of the quadratic function is 1. So the parabola opens up.

Since the parabola opens up and it does not intersect x-axis, the parabola is above the x-axis. So, the y-coordinates in all the points on the parabola will be greater than zero and and x-coordinate can be any real number.

Therefore, (1) is false and there is NO solution for the given quadratic inequality.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.