SOLVING QUADRATIC EQUATIONS BY FACTORING METHOD

(i) In a quadratic equation in the form ax² + bx + c  =  0, if the leading coefficient is 1, we have to decompose the constant term "c" into two factors.

(ii) The product of the two factors must be equal to the constant term "c" and the addition of two factors must be equal to the coefficient of x, that is "b".

(iii) If p and q are the two factors of the constant term c, then we have to factor the quadratic equation using p and q as shown below.

(x + p)(x + q)  =  0

(iv) Solving the above equation, we get

x  =  -p  and  x  =  -q

How to assign signs for the two factors ?

Solved Questions

Question 1 :

Solve the following quadratic equations by factorization method.

4x² - 7x - 2  =  0

Solution :

Product of coefficient of x²  and constant is -8

Now, we have to decompose -8 as product of two term, such that the product of those numbers must be -8 and simplified value must be equal to -7.

Since the middle and last terms are negative, we have to put negative sign for large factor.

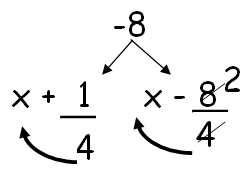
(4x + 1) (x - 2)  =  0

4x + 1  =  0   (or)   x - 2  =  0

  4x  =  -1   (or)    x = 2

   x  =  -1/4   (or)  x = 2

Hence the solutions are -1/4 and 2.

Question 2 :

Solve the following quadratic equations by factorization method.

3(p² - 6)  =  p(p + 5)

Solution :

 3p² - 18  =  p² + 5p

  3p² - p² - 5p - 18  =  0

  2p² - 5p - 18  =  0

Since the middle and last terms are negative, we have to put negative sign for large factor.

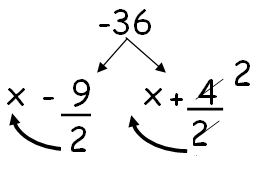
(2x + 9) (x - 2)  =  0

2x + 9  =  0    (or)  x - 2  =  0

2x  = -9    (or)  x = 2

 x  =  -9/2

Hence the solutions are -9/2 and 2.

Question 3 :

Solve the following quadratic equations by factorization method.

√[a(a -7)]  =  3√2

Solution :

√[a(a - 7)]  =  3√2

Taking squares on both sides,

[√(a(a - 7))]²  =  (3√2)²

a (a - 7)  =  9(2)

a² - 7a  =  18

a² - 7a  - 18  =  0

Since the middle and last terms are negative, we have to put negative sign for large factor.

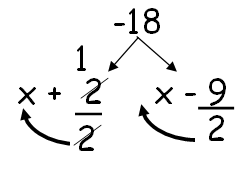
(x + 1) (2x - 9)  =  0

x + 1  =  0     (or)   2x - 9  =  0

x  =  -1    (or)  2x  =  9

                         x  =  9/2

Hence the solutions are -1 and 9/2.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.