SOLVING QUADRATIC EQUATIONS BY FACTORING EXAMPLES

Generally we have two types of quadratic equation.

• Quadratic equation of leading coefficient 1.
• Quadratic equation of leading coefficient not equal to 1. 

The general form of a quadratic equation is

ax² + bx + c  =  0

In a quadratic equation, leading coefficient is nothing but the coefficient of x².

Solving Quadratic Equations by Factoring with a Leading Coefficient of 1 - Procedure

(i) In a quadratic equation in the form ax² + bx + c  =  0, if the leading coefficient is 1, we have to decompose the constant term "c" into two factors.

(ii) The product of the two factors must be equal to the constant term "c" and the addition of two factors must be equal to the coefficient of x, that is "b".

(iii) If p and q are the two factors of the constant term c, then we have to factor the quadratic equation using p and q as shown below.

(x + p)(x + q)  =  0

(iv) Solving the above equation, we get

x  =  -p  and  x  =  -q

How to assign signs for the two factors ?

Solving Quadratic Equations by Factoring  when Leading Coefficient is not 1 - Procedure

(i) In a quadratic equation in the form ax² + bx + c  =  0, if the leading coefficient is not 1, we have to multiply the coefficient of x² and the constant term. That is "ac". Then, decompose "ac" into two factors.   

(ii) The product of the two factors must be equal to "ac" and the addition of two factors must be equal to the coefficient of x, that is "b".

(iii) Divide the two factors by the coefficient of x² and  simplify as much as possible.

(iv) Write the remaining number along with x (This is explained in the following example). 

Example 1 :

Solve for x : 

x² + 9x + 14  =  0

Solution :

In the given quadratic equation, the coefficient of x² is 1.

Decompose the constant term +14 into two factors such that the product of the two factors is equal to +14 and the addition of two factors is equal to the coefficient of x, that is +9. 

Then, the two factors of +14 are 

+2 and +7

Factor the given quadratic equation using +2 and +7 and solve for x.

(x + 2)(x + 7)  =  0

x + 2  =  0  or  x + 7  =  0

x  =  -2  or  x  =  -7

So, the solution is {-2, -7}. 

Example 2 :

Solve for x : 

x² - 9x + 14  =  0

Solution :

In the given quadratic equation, the coefficient of x² is 1.

Decompose the constant term +14 into two factors such that the product of the two factors is equal to +14 and the addition of two factors is equal to the coefficient of x, that is -9. 

Then, the two factors of +14 are 

-2 and -7

Factor the given quadratic equation using -2 and -7 and solve for x.

(x - 2)(x - 7)  =  0

x - 2  =  0  or  x - 7  =  0

x  =  2  or  x  =  7

So, the solution is {2, 7}. 

Example 3 :

Solve for x : 

x² + 2x - 15  =  0

Solution :

In the given quadratic equation, the coefficient of x² is 1.

Decompose the constant term -15 into two factors such that the product of the two factors is equal to -15 and the addition of two factors is equal to the coefficient of x, that is +2. 

Then, the two factors of -15 are 

+5 and -3

Factor the given quadratic equation using +5 and -3 and solve for x.

(x + 5)(x - 3)  =  0

x + 5  =  0  or  x - 3  =  0

x  =  -5  or  x  =  3

So, the solution is {-5, 3}. 

Example 4 :

Solve for x : 

x² - 2x - 15  =  0

Solution :

In the given quadratic equation, the coefficient of x² is 1.

Decompose the constant term -15 into two factors such that the product of the two factors is equal to -15 and the addition of two factors is equal to the coefficient of x, that is -2. 

Then, the two factors of -15 are 

+3 and -5

Factor the given quadratic equation using +3 and -5 and solve for x.

(x + 3)(x - 5)  =  0

x + 3  =  0  or  x - 5  =  0

x  =  -3  or  x  =  5

So, the solution is {-3, 5}. 

Example 5 :

Solve for x : 

2x² + 15x + 27  =  0

Solution :

In the given quadratic equation, the coefficient of x² is not 1.

So, multiply the coefficient of x² and the constant term "+27". 

3 ⋅ (+27)  =  +54

Decompose +54 into two factors such that the product of two factors is equal to +54 and the addition of two factors is equal to the coefficient of x, that is +15.

Then, the two factors of +54 are 

+6 and +9

Now we have to divide the two factors +6 and +9 by the coefficient of x², that is 2.

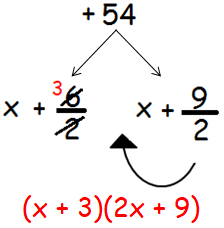
(x + 3)(2x + 9)  =  0

x + 3  =  0  or  2x + 9  =  0

x  =  -3  or  x  =  -9/2

So, the solution is {-3, -9/2}. 

Example 6 :

Solve for x : 

2x² - 15 x + 27  =  0

Solution :

In the given quadratic equation, the coefficient of x² is not 1.

So, multiply the coefficient of x² and the constant term "+27". 

3 ⋅ (+27)  =  +54

Decompose +54 into two factors such that the product of two factors is equal to +54 and the addition of two factors is equal to the coefficient of x, that is +15.

Then, the two factors of +54 are 

-6 and -9

Now we have to divide the two factors -6 and -9 by the coefficient of x², that is 2.

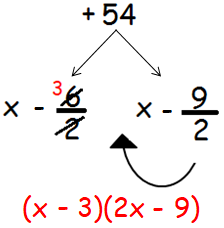
(x - 3)(2x - 9)  =  0

x - 3  =  0  or  2x - 9  =  0

x  =  3  or  x  =  9/2

So, the solution is {3, 9/2}. 

Example 7 :

Solve for x :

2x² + 3x - 27  =  0

Solution :

In the given quadratic equation, the coefficient of x² is not 1.

So, multiply the coefficient of x² and the constant term "-27". 

3 ⋅ (-27)  =  -54

Decompose -54 into two factors such that the product of two factors is equal to -54 and the addition of two factors is equal to the coefficient of x, that is +3.

Then, the two factors of -54 are 

+9 and -6

Now we have to divide the two factors +9 and -6 by the coefficient of x², that is 2.

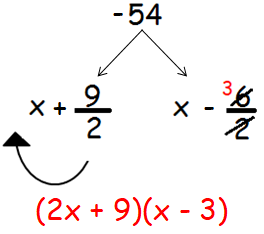
(2x + 9)(x - 3)  =  0

2x + 9  =  0  or  x - 3  =  0

x  =  -9/2  or  x  =  3

So, the solution is {-9/2, 3}. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.