SOLVING QUADRATIC EQUATION BY GRAPHING

In this section, you will learn how to solve a quadratic using its graph. 

To solve quadratic equation by graphing, we have to write the given quadratic equation as a quadratic function as shown below.

y  =  ax² + bx + x

Now, we can graph the above quadratic function by making the table of values. 

If the graph intersects x-axis in two points, then the quadratic equation has two roots. 

If the graph intersects (touches) x-axis in one point, then the quadratic equation has only one root.

If the graph does not intersect x-axis, then the quadratic equation has no real root. 

Solved Examples

Example 1 :

Solve the following quadratic equation by graphing : 

x² + 6x + 7 = 0

Solution :

Let y  =  x² + 6x + 7 -----(1)

Find the vertex of the quadratic function :

Comparing x² + 6x + 7 = 0 with ax² + bx + c = 0,  

a  =  1, b  =  6 and c  =  -7

x-coordinate of the vertex  =  -b/2a

x  =  -6/2(1)

x  =  -6/2

x  =  -3

Substitute x = -3 in (1) to find the y-coordinate of the vertex. 

y  =  (-3)² + 6(-3) - 7

y  =  9 - 18 - 7

y  =  -16

So, the vertex is (-3, -16)

Make a table of values to find other points to sketch the graph.

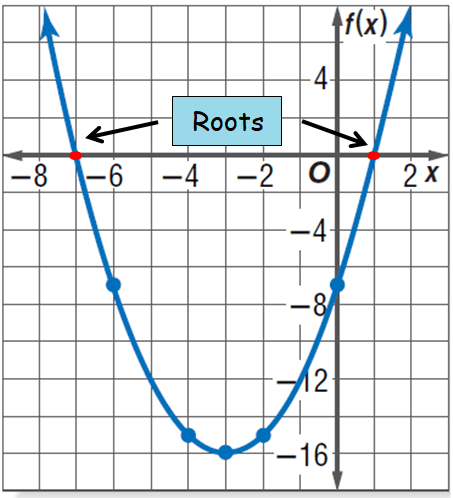
The graph above intersects intersects x-axis at 

x  =  -7  and  x  =  1

So, the solution is {-7, 1}. 

Example 2 :

Solve the following quadratic equation by graphing : 

x² + x + 4  =  0

Solution :

Let y  =  x² + x + 4 -----(1)

Find the vertex of the quadratic function :

Comparing x² + x + 4 = 0 with ax² + bx + c = 0,  

a  =  1, b  =  1 and c  =  4

x-coordinate of the vertex  =  -b/2a

x  =  -1/2(1)

x  =  -1/2

Substitute x = -1/2 in (1) to find the y-coordinate of the vertex. 

y  =  (-1/2)² + (-1/2) + 4

y  =  1/4 - 1/2 + 4

y  =  (1 - 2 + 16)/4

y  =  15/4  

So, the vertex is (-1/2, 15/4)

Make a table of values to find other points to sketch the graph.

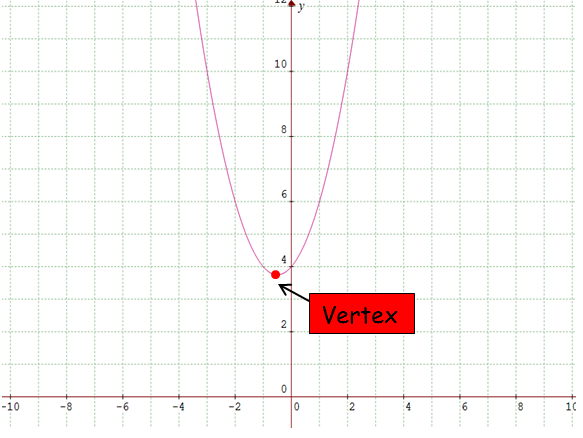
The graph above does not intersect x-axis. 

So, there is no real solution for the given quadratic equation. 

Example 3 :

Solve the following quadratic equation by graphing : 

x² - 7x + 6  =  0

Solution :

Step 1 :

Let y  =  x² - 7x + 6 -----(1)

Find the vertex of the quadratic function :

Comparing x² - 7x + 6 = 0 with ax² + bx + c = 0,  

a  =  1, b  =  -7 and c  =  6

x-coordinate of the vertex  =  -b/2a

x  =  -(-7)/2(1)

x  =  7/2

Substitute x = 7/2 in (1) to find the y-coordinate of the vertex. 

y = (7/2)² - 7(7/2) + 6

y = 49/4 - 49/2 + 6

y  =  (49 - 98 + 24)/4

y  =  -25/4  

So, the vertex is (7/2, -25/4)

Make a table of values to find other points to sketch the graph.

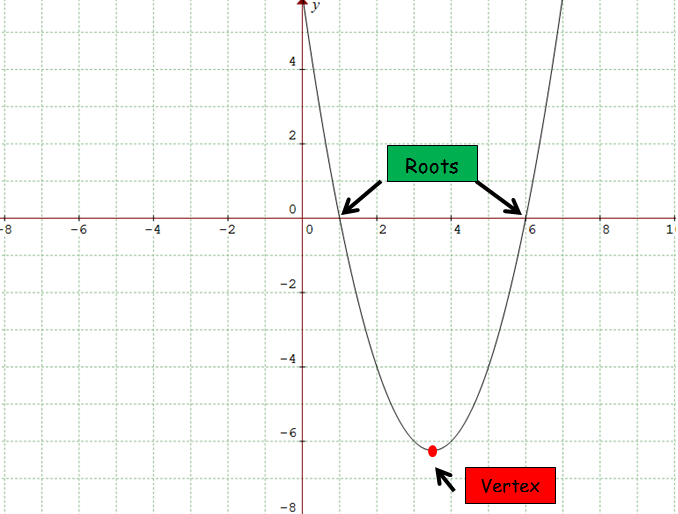
The graph above intersects intersects x-axis at 

x  =  1  and  x  =  6

So, the solution is {1, 6}.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.