SOLVING PROBLEMS WITH VECTORS

Problem 1 :

Show that the vectors a = 2i + 3j + 6k, b = 6i + 2j − 3k, and c = 3i − 6j + 2k are mutually orthogonal.

Solution :

Mutually orthogonal means, they are perpendicular to each other.

a vector ⋅ b vector = (2i + 3j + 6k) ⋅ (6i + 2j − 3k)

= 2(6) + 3(2) + 6(-3)

= 12 + 6 - 18

= 18 - 18

= 0

b vector ⋅ c vector = (6i + 2j − 3k) ⋅ (3i − 6j + 2k)

= 6(3) + 2(-6) + (-3)2

= 18 - 12 - 6

= 18 - 18

= 0

c vector ⋅ a vector = (3i − 6j + 2k) ⋅ (2i + 3j + 6k)

= 3(2) + (-6)(3) + 2(6)

= 6 - 18 + 12

= 18 - 18

= 0

Since, a ⋅ b = b ⋅ c = c ⋅ a = 0, the given vectors are mutually orthogonal.

Problem 2 :

Let -i - 2j - 6k,  2i - j + k, and -i + 3j + 5k be the sides of a triangle. Show that the above vectors form a right triangle. 

Solution :

The given vectors are the sides of a right triangle. To show that the triangle is a right triangle, it is enough to prove that the two of its sides are perpendicular. 

Let

a = -i - 2j - 6k

b = 2i - j + k 

c = = -i + 3j + 5k

a ⋅ b = (-i - 2j - 6k) ⋅ (2i - j + k)

= -1(2) + (-2)(-1) + (-6)(1)

= -2 + 2 - 6

= -6 ≠ 0

b ⋅ c = (2i - j + k) ⋅ (-i + 3j + 5k)

  = 2(-1) + (-1)(3) + 1(5)

= -2 - 3 + 5

= 0

Since b ⋅ c = 0, b vector and c vector are perpendicular.

So, the given vectors form a right triangle. 

Problem 3 :

If |a vector| = 5, |b vector| = 6, |c vector| = 7 and a vector + b vector + c vector  = 0 vector, find a ⋅ b + b ⋅ c + c ⋅ a .

Solution :

a vector + b vector + c vector = 0 vector

|a vector + b vector + c vector| = 0

Take square on both sides.

|a vector + b vector + c vector|² = 0²

|a|² + |b|² + |c|² + 2(a ⋅ b) + 2(b ⋅ c) + 2(c ⋅ a) = 0

|a|² + |b|² + |c|² + 2(a ⋅ b + b ⋅ c + c ⋅ a) = 0

Substitute the given values. 

5² + 6² + 7² + 2(a ⋅ b + b ⋅ c + c ⋅ a) = 0

25 + 36 + 49 + 2(a ⋅ b + b ⋅ c + c ⋅ a) = 0

110 + 2(a ⋅ b + b ⋅ c + c ⋅ a) = 0

Subtract 110 from each side. 

2(a ⋅ b + b ⋅ c + c ⋅ a) = -110

Divide each side by 2. 

a ⋅ b + b ⋅ c + c ⋅ a = -55

Problem 4 :

Show that the points (2, - 1, 3), (4, 3, 1) and (3, 1, 2) are coplanar.

Solution :

Let

a = 2i - j + 3k

b = 4i + 3j + k

c = 3i + j + 2k

If, three vectors are collinear, then their scalar product is zero. 

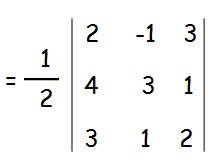
= (1/2)[2(6 - 1) + 1(8 - 3) + 3(4 - 9)]

= (1/2)[ 2(5) + 1(5) + 3(-5)]

= (1/2) [10 + 5 - 15]

= (1/2)[15 - 15]

= 0

Since the scalar product of the three vectors a, b and c zero, the given points are coplanar.

Problem 5 :

If a vector, b vector are unit vectors and θ is the angle between them, show that

(i) sin(θ/2) = (1/2)|a vector - b vector|

Solution :

In the first step, let us take square for |a vector - b vector|.

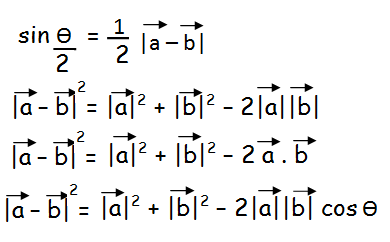
Since a vector and b vector are unit vectors, we have to apply 1 instead of a vector and b vector.

|a vector - b vector|² = 1² + 1² - 2(1)(1)cosθ

|a vector - b vector|² = 2 - 2cosθ

|a vector - b vector|² = 2(1- cosθ)

|a vector - b vector|² = 2 (2sin² (θ/2))

|a vector - b vector| = 2sin(θ/2)

sin(θ/2) = (1/2)|a vector - b vector| ----(1)

Hence it is proved

(ii) cos(θ/2) = (1/2) |a vector + b vector|

Solution :

In the first step, let us take square for |a vector + b vector|

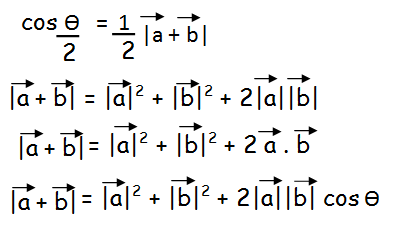
Since a vector and b vector are unit vectors, we have to apply 1 instead of a vector and b vector.

|a vector + b vector|² = 1² + 1² + 2(1)(1)cosθ

|a vector - b vector|² = 2 + 2cosθ

|a vector - b vector|² = 2(1 + cosθ)

|a vector - b vector|² = 2(2 cos²(θ/2))

|a vector - b vector| = 2cos(θ/2)

cos(θ/2) = (1/2)|a vector + b vector| ----(2)

Hence it is proved

(ii) tan(θ/2) = |a vector-b vector| / |a vector-b vector|

Solution :

We may prove the above result using (1) and (2).

sin(θ/2) = (1/2)|a vector - b vector|

cos(θ/2) = (1/2)|a vector + b vector|

(1)/(2) : 

sin(θ/2)/cos(θ/2)

= (1/2)|a vector - b vector|/(1/2)|a vector + b vector|

tan(θ/2)

= (1/2)|a vector - b vector|/(1/2)|a vector + b vector|

Problem 6 :

Let a vector, b vector, c vector be three vectors such that |a vector| = 3, |b vector|= 4, |c vector|= 5, If all the three vectors are perpendicular to each other, find the value of | a vector + b vector + c vector|. 

Solution :

|a + b + c|² = |a|² + |b|² + |c|² + 2(a ⋅ b + b ⋅ c + c ⋅ a)

Substitute the given values. 

= 3² + 4² + 5² + 2(a ⋅ b + b ⋅ c + c ⋅ a)

Since the three a, b and c are perpendicular to each other, a ⋅ b = b ⋅ c = c ⋅ a = 0. 

= 9 + 16 + 25 + 2(0 + 0 + 0)

|a + b + c|² = 50

|a + b + c| = √50

|a + b + c| = 5√2

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.