HOW TO SOLVE POLYNOMIAL EQUATION OF DEGREE 5
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
To solve a polynomial equation of degree 5, we have to factor the given polynomial as much as possible. After having factored, we can equate factors to zero and solve for the variable.
Example 1 :
Solve :
6x5 - x4 - 43x3 + 43x2 + x - 6 = 0
Solution :
By trial and error, we can check the values 1 or -1 or 2 or -2...... as a zero for the above equation using synthetic division.
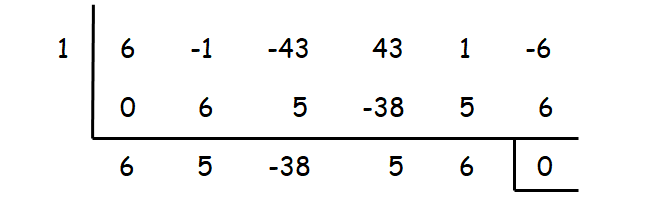
When we check with the value 1, we get remainder zero. So, x = 1 is one of the zeros.
Resulting equation :
6x4 + 5x3 - 38x2 + 5x + 6 = 0
Dividing both sides by x2.
6x4/x2 + 5x3/x2 - 38x2/x2 + 5x/x2 + 6/x2 = 0
6x2 + 5x - 38 + 5/x + 6/x2 = 0
6(x2 + 1/x2) + 5 (x + 1/x) - 38 = 0 ----(1)
Let y = x + 1/x.
y2 = (x + 1/x)2
y2 = x2 + 2(x)(1/x) + (1/x)2
y2 = x2 + 2 + 1/x2
y2 - 2 = x2 + 1/x2
(1)----> 6(y2 - 2) + 5y - 38 = 0
6y2 - 12 + 5y - 38 = 0
6y2 + 5y - 50 = 0
6y2 - 15y + 20 y - 50 = 0
3y(2y - 5) + 10(2y - 5) = 0
(3y + 10)(2y - 5) = 0
|
3y + 10 = 0 y = -10/3 |
2y - 5 = 0 y = 5/2 |
When y = -10/3,
(x2 + 1)/x = -10/3
3(x2 + 1) = -10x
3x2 + 3 = -10x
3x2 + 10x + 3 = 0
(3x + 1)(x + 3) = 0
x = -1/3 and 3
When y = 5/2,
x + 1/x = y
(x2 + 1)/x = 5/2
2(x2 + 1) = 5 x
2x2 + 2 - 5x = 0
2x2 - 5x + 2 = 0
(2x - 1)(x - 2) = 0
x = 1/2 and 2
Therefore the five zeros are 1, -1/3, 3, 1/2 and 2.
Example 2 :
Solve :
8x5 - 22x4 - 55x3 + 55x2 + 22x - 8 = 0
Solution :
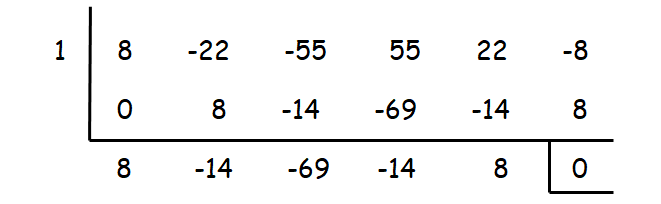
When we check with the value 1, we get remainder zero. So, x = 1 is one of the zeros.
Resulting equation :
8x4 - 14x3 - 69x2 - 14x + 8 = 0
Dividing both sides by x2.
8x4/x2 - 14x3/x2 - 69x2/x2 - 14x/x2 + 8/x2 = 0
8x2 - 14x - 69 - 14/x + 8/x2 = 0
8(x2 + 1/x2) - 14(x + 1/x) - 69 = 0 ----(1)
Let y = x + 1/x.
y2 = (x + 1/x)2
y2 = x2 + 2(x)(1/x) + (1/x)2
y2 = x2 + 2 + 1/x2
y2 - 2 = x2 + 1/x2
(1)----> 8(y2 - 2) - 14y - 69 = 0
8y2 - 16 - 14y - 69 = 0
8y2 - 14y - 85 = 0
(2y + 5)(4y - 17) = 0
|
2y + 5 = 0 y = -5/2 |
4y - 17 = 0 y = 17/4 |
When y = -5/2,
x + 1/x = y
(x2 + 1)/x = -5/2
2(x2 + 1) = -5x
2x2 + 2 + 5x = 0
2x2 + 5x + 2 = 0
2x2 + 4x + 1x + 2 = 0
2x(x + 2) + 1(x + 2) = 0
(2x + 1)(x + 2) = 0
x = -1/2 and -2
When y = 17/4,
x + 1/x = y
(x2 + 1)/x = 17/4
4(x2 + 1) = 17x
4x2 + 4 = 17x
4x2 - 17x + 4 = 0
(4x - 1)(x - 4) = 0
x = 1/4 and 4
Therefore the five zeros are 1, -1/2, -2, 1/4 and 4.
Example 3 :
Solve :
6x5 + 11x4 - 33x3 - 33x2 + 11x + 6 = 0
Solution :
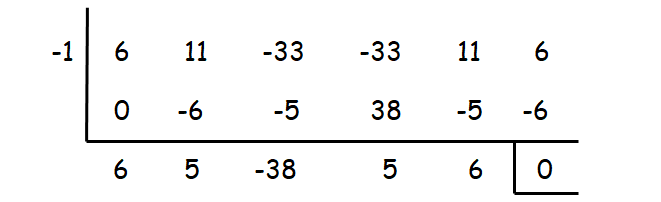
When we check with the value -1, we get remainder zero. So, x = -1 is one of the zeros.
Resulting equation :
6x4 + 5x3 - 38x2 + 5x + 6 = 0
Dividing both sides by x2.
6x4/x2 + 5x3/x2 - 38x2/x2 + 5x/x2 + 6/x2 = 0
6x2 + 5x - 38 + 5/x + 6/x2 = 0
6(x2 + 1/x2) + 5(x + 1/x) - 38 = 0 ----(1)
Let y = x + 1/x.
y2 = (x + 1/x)2
y2 = x2 + 2(x)(1/x) + (1/x)2
y2 = x2 + 2 + 1/x2
y2 - 2 = x2 + 1/x2
(1)----> 6(y2 - 2) + 5y - 38 = 0
6y2 - 12 + 5y - 38 = 0
6y2 + 5y - 50 = 0
6y2 - 15y + 20y - 50 = 0
3y(2y - 5) + 10(2y - 5) = 0
(3y + 10)(2y - 5) = 0
|
3y + 10 = 0 y = -10/3 |
2y - 5 = 0 y = 5/2 |
When y = -10/3,
x + 1/x = y
(x2 + 1)/x = -10/3
3(x2 + 1) = -10x
3x2 + 3 = -10x
3x2 + 10x + 3 = 0
3x2 + 9x + x + 3 = 0
3x(x + 3) + 1(x + 3) = 0
(x + 3)(3x + 1) = 0
x = -3 and -1/3
When y = 5/2,
x + 1/x = y
(x2 + 1)/x = 5/2
2(x2 + 1) = 5x
2x2 + 2 - 5x = 0
2x2 - 5x + 2 = 0
2x2 - 4x - x + 2 = 0
2x(x - 2) - 1(x - 2) = 0
(2x - 1)(x - 2) = 0
x = 1/2 and 2
Therefore the five zeros are -1, -3, -1/3, 1/2 and 2.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4)
