SOLVING POLYNOMIAL EQUATIONS WITH DIFFERENT POWERS

Question 1 :

Solve the following equations

(i) sin² x − 5sin x + 4 = 0

Solution :

Let y = sin x

y² − 5 y + 4 = 0

(y - 1) (y - 4)  =  0

y  =  1 and y  =  4

(ii) 12x³ + 8x = 29x² − 4

Solution :

12x³ + 8x = 29x² − 4

12x³ - 29x² + 8x + 4  =  0

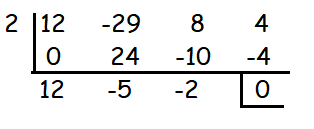
(x - 2) is a factor.The other factors are 12x² - 5x - 2

12x² - 5x - 2  =  0

12x² - 8x + 3x - 2  =  0

4x(3x - 2) + 1(3x - 2)  =  0

(4x + 1) (3x - 2)  =  0

So, the factors are (x - 2) (4x + 1) (3x - 2)

x - 2  =  0, 4x + 1  =  0, 3x - 2  =  0

x  =  2, x  =  -1/4, x  =  2/3

Hence 2, -1/4 and 2/3 are roots of the given polynomial.

Let a_n xⁿ + ........ + a₁x + a0 with a_n ≠ 0 and, be a polynomial with integer coefficients. If p/q, with ( p, q) =1, is a root of the polynomial, then p is a factor of a₀ and q is a factor of a_n .

Question  2 :

Examine for the rational roots of

(i) 2x³ − x² − 1 = 0

Solution :

Factor of 1 are ± 1 = p

Factor of 2 are ±1 and ±2 = q

p/q  =  1/1, 1/2, -1/1, -1/2

If the given equation will have rational solution, then it must be one of the above given solutions.

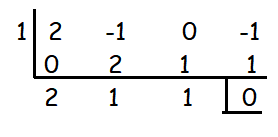
1 is the rational number and it is the factor of the given polynomial. 1/2 is not the factor of the given polynomial.

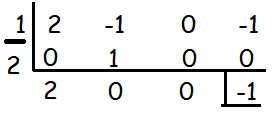
Hence the given polynomial has rational roots.

(ii) x⁸ − 3x + 1 = 0

Solution :

Factor of 1 are ± 1 (the constant) = p

Factor of 1 are ±1 (coefficient of x⁸) = q

p/q  =  1, -1

If the given equation will have rational solution, then it must be one of the above given solutions.

Hence the given polynomial will not have rational roots.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.