SOLVING POLYNOMIAL AND NON POLYNOMIAL EQUATIONS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Example 1 :
Solve :
8x3/2n - 8x-3/2n = 63
Solution :
8x3/2n - 8x-3/2n = 63
8x3/2n - 8(1/x3/2n) = 63
Divide both sides by 8.
x3/2n - (1/x3/2n) = 63/8
Let t = x3/2n.
t - (1/t) = 63/8
8(t2 - 1) = 63t
8t2 - 63t - 8 = 0
8t2 - 64t + t - 8 = 0
8t(t - 8) + 1(t - 8) = 0
(8t + 1)(t - 8) = 0
t = -1/8 and t = 8
When t = -1/8,
x3/2n = -1/8
Take power 2n/3 on both sides.
(x3/2n)2n/3 = (-1/8)2n/3
x = (-1/8)2n/3
x = [(-1/2)3]2n/3
x = (-1/2)2n
x = [(-1/2)2]n
x = (1/4)n
x = 1/4n
But x = 1/4n will not satisfy the given equation. So, we can ignore this solution.
When t = 8,
x3/2n = 8
Take power 2n/3 on both sides.
(x3/2n)2n/3 = 82n/3
x = 82n/3
x = (23)2n/3
x = 22n
x = (22)n
x = 4n
The possible solution is x = 4n.
Example 2 :
Solve :
2√(x/a) + 3√(a/x) = b/a + 6a/b
Solution :
Let t = √(x/a). Then, 1/t = √(a/x).
2√(x/a) + 3√(a/x) = b/a + 6a/b
2t + 3(1/t) = b/a + 6a/b
2t + 3/t = b/a + 6a/b
Multiply both sides by abt.
2t2ab + 3ab = b2t + 6a2t
2t2ab + 3ab = (b2 + 6a2)t
2t2ab - (b2 + 6a2)t - 3ab = 0
Solve the above quadratic equation in the variable 't' using quadratic formula.
t = [-b ± √(b2 - 4ac)]/2a
t = [(b2 + 6a2) ± √(b2 + 6a2)2 - 4(2ab)(3ab)]/2(2ab)
t = [(b2 + 6a2) ± √(b4 + 36a4 + 12a2b2 - 24a2b2)/4ab
t = [(b2 + 6a2) ± √(b2-6a2)2]/4ab
t = [(b2 + 6a2) ± (b2-6a2)]/4ab
t = [(b2 + 6a2) + (b2-6a2)]/4ab
|
t = (b2+6a2)+(b2-6a2)/4ab t = 2b2/4ab t = b/2a √(x/a) = t x/a = (b/2a)2 x = ab2/4a2 x = b2/4a |
t = (b2+6a2)-(b2-6a2)/4ab t = 12a2/4ab t = 3a/b √(x/a) = t x/a = (3a/b)2 x = 9a3/b2 |
Example 3 :
Solve :
6x4 - 35x3 + 62x2 - 35x + 6 = 0
Solution :
This is a polynomial equation of degree 4. So, we will have four zeros.
By trial and error, we can check the values 1 or -1 or 2 or -2...... as zeros for the above equation using synthetic division.
6x4 - 35x3 + 62x2 - 35x + 6 = 0
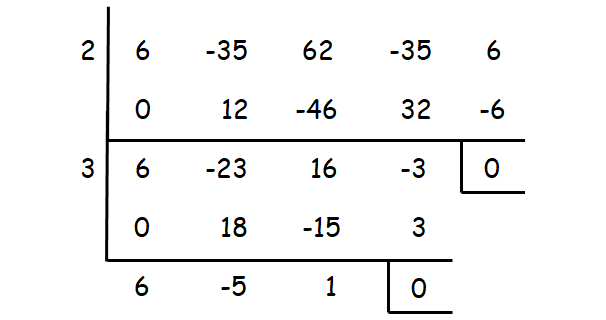
2 and 3 are the two zeros of the given equation. To get the other two zeros, solve the resulting quadratic equation in the above synthetic division.
6x2 - 5x + 1 = 0
6x2 - 2x - 3x + 1 = 0
2x(3x - 1) - 1(3x - 1) = 0
(2x - 1)(3x - 1) = 0
x = 1/2 and 1/3
The four zeros are 2, 3, 1/2 and 1/3.
Example 4 :
Solve :
x4 + 3x3 - 3x - 1 = 0
Solution :
This is a polynomial equation of degree 4. So, we will have four zeros.
By trial and error, we can check the values 1 or -1 or 2 or -2...... as zeros for the above equation using synthetic division.
x4 + 3x3 - 3x - 1 = 0
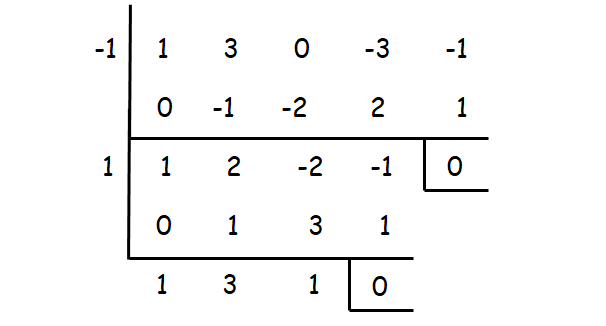
1 and -1 are the two zeros of the given equation. To get the other two zeros, solve the resulting quadratic equation in the above synthetic division.
x2 + 3x + 1 = 0
x = [-b ± √(b2 - 4ac)]/2a
x = [-3 ± √(9 - 4)]/2(1)
x = (-3 ± √5)/2
The four zeros are -1, 1, (-3 + √5)/2 and (-3 - √5)/2.
Example 5 :
Find all real numbers satisfying 4x - 3(2x + 2) + 25 = 0.
Solution :
4x - 3(2x + 2 ) + 25 = 0
(22)x - 3(2x22) + 32 = 0
(2x)2 - 12(2x) + 32 = 0
Let y = 2x.
y2 - 12y + 32 = 0
y2 - 8y - 4y + 32 = 0
y(y - 8) - 4(y - 8) = 0
(y - 4)(y - 8) = 0
y = 4 and 8
|
y = 4 2x = 4 2x = 22 x = 2 |
2x = 8 2x = 23 x = 3 |
The two zeros are 2 and 3.
Example 6 :
Solve the equation 6x4 - 5x3 - 38x2 - 5x + 6 = 0 if it is known that 1/3 is a solution.
Solution :
Given : 1/3 is a solution.
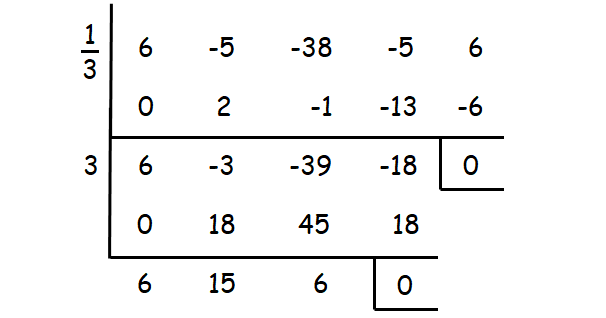
1/3 and 3 are the two zeros of the given equation. To get the other two zeros, solve the resulting quadratic equation in the above synthetic division.
6x2 + 15x + 6 = 0
6x2 + 12x + 3x + 6 = 0
6x(x + 2) + 3(x + 2) = 0
(6x + 3)(x + 2) = 0
x = -1/2 and -2
The solutions are 1/3, 3, -1/2 and -2.
Example 7 :
If (ax + 2)(bx + 7) = 15x2 + cx + 14 for all values of x and a + b = 8, what are the two possible values of c ?
Solution :
(ax + 2)(bx + 7) = 15x2 + cx + 14
abx2 + 7ax + 2bx + 14 = 15x2 + cx + 14
abx2 + (7a + 2b)x + 14 = 15x2 + cx + 14
ab = 15 ----(1)
7a + 2b = c ------(2)
a + b = 8 ------(3)
b = 8 - a
a(8 - a) = 15
8a - a2 = 15
a2 - 8a + 15 = 0
(a - 3) (a - 5) = 0
a = 3 and a = 5
When a = 3, b = 8 - 3 ==> 5
When a = 5, b = 8 - 5 ==> 3
Applying the values of a and b in (2), we get
|
7(3) + 2(5) = c c = 21 + 10 c = 31 |
7(5) + 2(3) = c c = 35 + 6 c = 41 |
So, the possible values of c are 31 and 41.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
10 Hard SAT Math Questions (Part - 38)
Dec 08, 25 12:12 AM
10 Hard SAT Math Questions (Part - 38) -
SAT Math Practice
Dec 05, 25 04:04 AM
SAT Math Practice - Different Topics - Concept - Formulas - Example problems with step by step explanation -
10 Hard SAT Math Questions (Part - 37)
Dec 03, 25 07:02 AM
10 Hard SAT Math Questions (Part - 37)


