SOLVING PERCENT PROBLEMS

Problem 1 :

What is 30 percent of 600? 

Solution :

The picture shown below clearly illustrates the answer for the given question. 

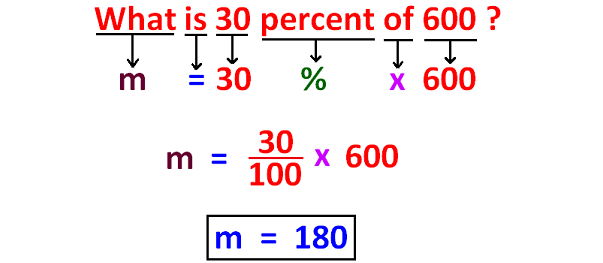
So, 30 percent of 600 is 180.

Problem 2 : 

What percent of 500 is 75 ? 

Solution :

The picture shown below clearly illustrates the answer for the given question. 

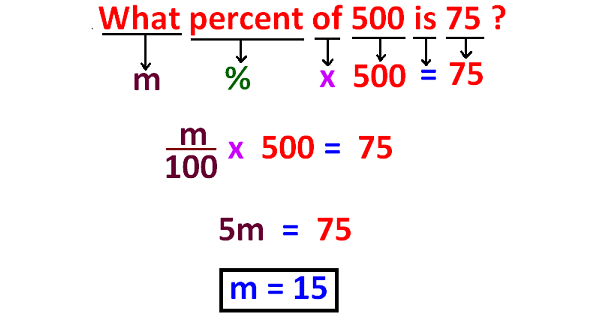
So, 15 percent of 500 is 75.

Problem 3 :

What percent of 29 is 3?

Solution :

Let x be the required percentage.

Then, we have

x% of 29 = 3

(x/100) ⋅ 29 = 3

29x/100 = 3

Multiply each side by 100/29.

x = 3 ⋅ (100/29)

x = 300/29

x ≈ 10.3%

So, about 10.3% of 29 is 3.

Problem 4 : 

Evaluate : 

147 ÷ 49%

Solution :

147 ÷ 49% = 147 ÷ 0.49

147 ÷ 49% = 147 / 0.49

147 ÷ 49% = 14700 / 49

147 ÷ 49% = 300

Problem 5 :

If 20% of k is 8, then  find the value of k.

Solution :

20% of k = 8

0.2 ⋅ k = 8

Divide each side by 0.2.

k = 40

Problem 6 :

An item is sold at 20% profit. If the cost price of the item is $80, find the selling price.

Solution :

selling Price = (100 + 20)% of cost price

Substitute $80 for cost price.

selling price = 120% of $80

= 1.2 ⋅ $80

= $96

Problem 7 :

An item is sold at 20% profit. If the selling price of the item is $108, find the cost price.

Solution :

(100 + 20)% of cost price = selling price

Substitute $108 for selling price.

120% of cost price = $108

1.2 ⋅ cost price = $108

Divide both sides by 1.2.

cost price = $90

Problem 8 :

Jacob spends 40% of his salary for food and 30% of the remaining for clothes and saves the rest. If Jacob's salary is $3000 per month, how much can he save in one year?

Solution :

Money spent for food :

40% of the salary = 0.4 ⋅ 3000

40% of the salary = $1200

Remaining salary is 

= $3000 - $1200

= $1800

Money spent for clothes :

30% of the remaining salary = 0.3 ⋅ 1800

30% of the remaining salary = $540

After $540 spent for cloth, amount of money remaining : 

= $1800 - $540

= $1260

After spent money for food and cloth, Jacob saves $1260 per month. 

Amount of money saved in one year : 

= 12 ⋅ 1260

= $15,120

Problem 9 :

Richard wants to earn a profit of 10 percent on selling an item at 12% percent discount. By what percent must he increase the cost price to get the list price ?

(List price = Price before discount given)

Solution :

Let $100 be the cost price of the item.

Then, the selling price of the item is 

= 1.1 ⋅ 100

= 110 -----(1)

Let x be the list price. 

Then, the selling price (after 12% discount in list price) is 

= 0.88x ----(2)

From (1) and (2), we get

0.88x = 110

Divide each side by 0.88.

x = 125

Therefore the list price is $125.

Percentage increase from 100 to 125 is 25%. 

So, Richard must increase 25 percent of the cost price to get the list list price. 

Problem 10 :

If 20% of (x + y) is 60 and 40% of x is 36, then find 70% of y.

Solution :

Given : 20% of (x + y) is 60.

0.2(x + y) = 60

Divide each side by 0.2

x + y = 300 ----(1)

Given : 40% of x is 36.

0.4x = 36

Divide each side by 0.4

x = 90

Substitute 90 for x in (1).

90 + y = 300

Subtract 90 from each side. 

y = 210

70% of y = 70% of 210 

70% of y = 0.7 ⋅ 210

70% of y = 147

Problem 11 :

A is 40% of B, C is 30% of B. What percent of A is C?

Solution :

Since B is linked to both A and C, we can assume some value for B and solve the problem.

Let B = 100.

Given : A is 20% of B.

A = 0.4(100)

A = 40

Given : C is 30% of B.

C = 0.3(100)

C = 30

Let y% of A be equal to C.

y% of A = C

ʸ⁄₁₀₀ ⋅ 40 = 30

Divide both sides by 40.

ʸ⁄₁₀₀ = 0.75

Multiply both sides by 100.

y = 75

Therefore, 75% of A is C.

Problem 12 :

A store sells all items at 30% off and 5% sales tax has to be paid for all the items sold. What percentage of the original price has to be paid for each item?

Solution :

Let $100 be the original price of an item.

Price  of  the item after 30% off :

= (100 - 30)% of $100

= 70% of $100

= 0.7 ⋅ $100

= $70

Amount has to be paid for the item after 5% sales tax :

= (100 + 5)% of $70

= 105% of $70

= 1.05 ⋅ $70

= $73.5

73.5 is 73.5% of 100.

Therefore, 73.5% of the original price has to be paid for each item.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.