SOLVING ONE STEP EQUATIONS

A one-step equation is as straightforward as it sounds. We just have to perform one step in order to solve the equation. 

We have to isolate the variable which comes in the equation. 

That is, we have to get rid of the number which is added to the variable or subtracted from the variable or multiplied by the variable or divides the variable. 

Examples 

Example 1 :

Solve for x :

5 + x  =  3

Solution : 

Here 5 is added to the variable x.

To get rid of 5, we have to subtract 5 from each side of the equation as shown below. 

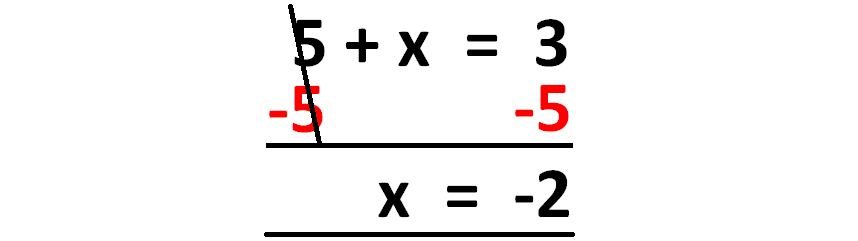
So, the value of x is -2. 

Example 2 :

Solve for p :  

p - 7  =  3

Solution : 

Here 7 is subtracted from the variable p.

To get rid of -7, we have to add 7 to each side of the equation as shown below.

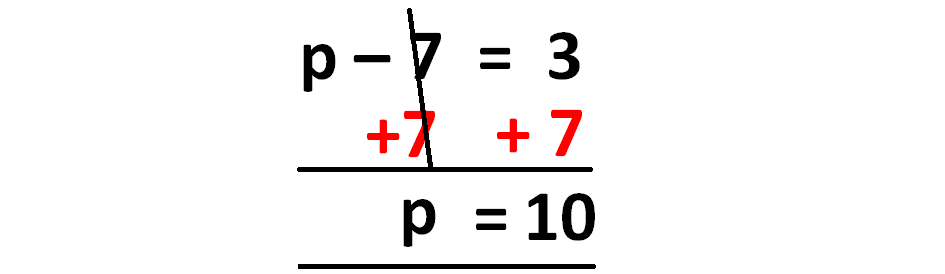
So, the vale of p is 10.

Example 3 :

Solve for r :  

2r  =  6

Solution : 

Here r is multiplied by 2.

To get rid of 2, we have to divide each side of the equation by 2 as shown below. 

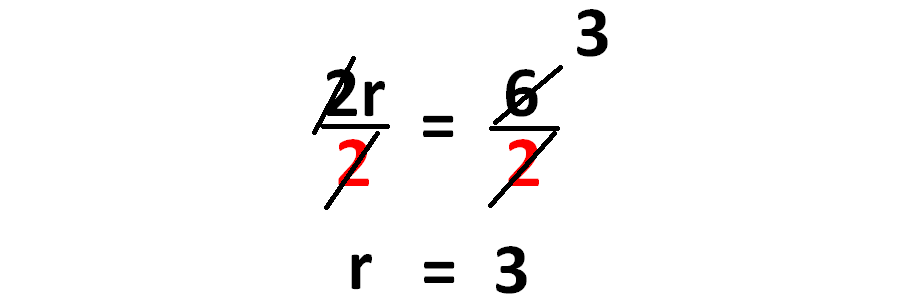
So, the vale of r is 3.

Example 4 :

Solve for m :  

(1/4)m  =  3

Solution : 

Here m is divided by 4.

To get rid of 4, we have to multiply each side of the equation by 4 as shown below.  

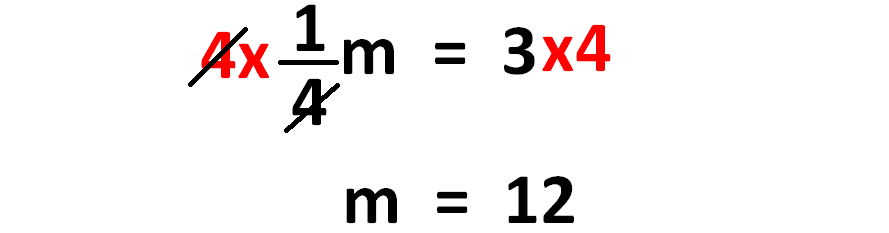
So, the vale of m is 12.

Example 5 :

Solve for p :  

8 - p  =  12

Solution : 

Here p is having negative sign.

In this problem, first we have to make p to be positive.

For that, we have to add p to each side of the equation. When we do so, we will have "12 + p" on the right side of the equation.

Then, to get rid of 12 on the right side, we have to subtract 12 from each side of the equation. 

Therefore, we have to add p and subtract 12 on both sides and solve the equation as shown below. 

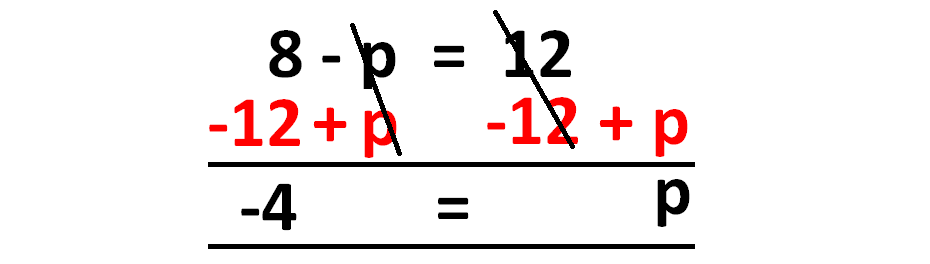
So, the vale of p is -4.

Example 6 :

Solve for m :

m - 10  =  -15

Solution : 

m - 10  =  -15

Add 10 to each side. 

m  =  -5

So, the value of m is -5. 

Example 7 :

Solve for v :

v + 5/3  =  - 1/3

Solution : 

v + 5/3  =  - 1/3

Subtract 5/3 from each side. 

v  =  -2

So, the value of v is -2.

Example 8 :

Solve for m :

38 - m  =  -44

Solution : 

Here m is having negative sign.

In this problem, first we have to make m to be positive.

For that, we have to add m to each side of the equation.

When we do so, we will have "-44 + m" on the right side of the equation.

Then, to get rid of -44 on the right side, we have to add 44 to each side of the equation.

Therefore, we have to add m and 44 to each side of the given equation.

Then, 

82  =  m

So, the value of m is 82.

Example 9 :

Solve for n :

11.7  =  1.1 + n

Solution : 

11.7  =  1.1 + n

Subtract 1.1 from each side. 

10.6  =  n

So, the value of n is 10.6.

Example 10 :

Solve for v :

-25.7 - v  =  -40.3

Solution : 

Add 25.7 on both sides,

-v  =  -40.3 + 25.7

-v  =  -14.6

Dividing by -1 on both sides, we get

v  =  14.6

So, the value of v is 40.3. 

Please click on the following links to download worksheets on solving one step equations. 

Worksheet -1

Worksheet -2

Worksheet -3

Worksheet -4

Worksheet -5

Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.