SOLVING MULTI STEP WORD PROBLEMS WORKSHEET

Problem 1 :

The numerator and denominator of a fraction add up to 17. If the denominator is 1 more than thrice the numerator, find the fraction. 

Problem 2 :

The age of a father is 13 more than 4 times the age of his son. If their ages add up to 48 years, find the ages of the son and father. 

Problem 3 :

In a two digit number, sum of the two digits is 13. The number formed by switching the digits is greater than the original number by 27. Find the number.

Problem 4 :

Tammy picks three sides of a rectangle and adds their lengths  to get 140 cm. Gladys picks three sides of the same rectangle and adds their lengths to get 100 cm. What is the perimeter of the rectangle in cm?

Problem 5 :

The ratio between the two liquids A and B in a liquid mixture of 75 liters is 2 : 3. If 5 more liters of liquid B is is added, find the amount of liquid A may be added so that the ratio between the liquids A and B in the mixture may change to 7 : 10.

Problem 6 :

In a triangle, the second angle is 5° more than twice the first angle and the third angle is 25° more than thrice the second angle. Find the three angles of the triangle.

Answers

1. Answer :

Step 1 :

Let x be the numerator of the fraction.

It is given that the denominator is 1 more than thrice the numerator.

Then, the denominator of the fraction is

= 3x + 1

The fraction is

Step 2 :

It is given that the numerator and denominator of a fraction add up to 17.

numerator + denominator = 17

x + (3x + 1) = 17

x + 3x + 1 = 17

4x + 1 = 17

4x = 16

x = 4

Step 3 :

Substitute x = 4 in (1).

3x + 1 = 3(4) + 1

= 12 + 1

= 13

Step 4 :

Substitute x = 4 in (1) to get the fraction.

2. Answer :

Step 1 :

Let x be the age of the son.

It is given that the age of a father is 13 more than 4 times the age of his son.

Then, the age of the father is 

= 4x + 13 ----(1)

Step 2 :

It is given that the sum of the ages of son and father is 48 years.

x + (4x + 13) = 48

x + 4x + 13 = 48

5x + 13 = 48

5x = 35

x = 7

Step 3 :

Substitute x = 7 in (1).

4x + 13 =  4(7) + 13

= 28 + 13

= 41

Step 4 :

Age of the son = 7 years

Age of the son = 41 years

3. Answer :

Step 1 :

Let xy be the two digit number.

It is given that the sum of the digits is 13.

x + y = 13 ----(1)

Step 2 :

It is given that the number formed by switching the digits is greater than the original number by 27.

yx = xy + 27

10(y) + 1(x) = 10(x) + 1(y) + 27

10y + x = 10x + y + 27

-9x + -9y = 27

-x + y = 3 ----(2)

Step 3 :

Solve (1) and (2) for x and y.

(1) + (2) :

2y = 16

y = 8

Substitute y = 8 in (1).

x + 8 = 13

x = 5

xy = 58

So, the required number is 58.

4. Answer :

Step 1 :

Let x and y be the length and width of the rectangle respectively.

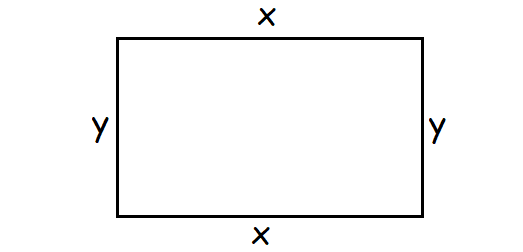
Step 2 :

Given : Tammy picks three sides of a triangle and adds their lengths  to get 140 cm.

Let's assume that Tammy picks two lengths and one width.

2x + y = 140 ----(1)

Step 3 :

Given : Gladys picks three sides of the same triangle and adds their lengths to get 100 cm.

Let's assume that Gladys picks one length and two widths.

x + 2y = 100 ----(2)

Step 4 :

(1) + (2) :

(2x + y) + (x + 2y) = 140 + 100

2x + y + x + 2y = 240

3x + 3y = 240

Divide both sides by 3.

x + y = 80

Multiply both sides by 2.

2(x + y) = 160

Therefore, perimeter of  the rectangle is 160 cm.

5. Answer :

Step 1 :

Sum of the terms in the given ratio 2 : 3 is

= 2 + 3

= 5

Step 2 :

Amount of liquid A in the mixture :

= 30 liters

Step 3 :

Amount of liquid B in the mixture :

= 45 liters

Step 4 :

Let x ml. be the amount of liquid A added in the mixture.

Given : Amount of liquid B added in the mixture is 5 ml.

Now, in the mixture,

amount of liquid A = (30 + x) ml

amount of liquid B = 45 + 5 = 50 ml 

Step 3 :

Given : The ratio after adding more liquids is 7 : 10.

(30 + x) : 50 = 7 : 10

10(30 + x) = 50(7)

300 + 10x = 350

10x = 50

x = 5

Amount of liquid A added in the mixture is 5 ml.

6. Answer :

Step 1 :

Let x be the first angle.

Given : The second angle is 5° more than twice the first angle and the third angle is 25° more than thrice the second angle.

Second angle = 2x + 5°

Third angle = 3(2x + 5°) + 25°

= 6x + 15° + 25°

= 6x + 40°

Step 2 :

Three angles of a triangle add up to 180°.

x + (2x + 5°) + (6x + 40°) = 180°

x + 2x + 5° + 6x + 40° = 180°

9x + 45° = 180°

9x = 135°

x = 15°

First Angle = 15°

Second Angle :

2x + 5° = 2(15°) + 5°

= 30° + 5°

= 35°

Third Angle :

6x + 40° = 6(15°) + 40°

= 90° + 40°

= 130°

So, the three angles of the triangle are 15°, 35° and 130°.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.