SOLVING LINEAR INEQUALITIES

The following steps will be useful to solve linear inequalities.

Step 1 :

Read and understand the information carefully and translate the statements into linear inequalities. 

Step 2 :

Solve for the variable using basic operations like addition, subtraction, multiplication and division.

Step 3 :

Find the solution set and obtain some of the possible solutions.

Apart from the above steps, we have to make the following changes, when we multiply or divide each side of the inequality by a negative value. 

•  If we have  <, then change it as  >
•  If we have  >, then change it as  <
•  If we have  ≤, then change it as  ≥
•  If we have  ≥, then change it as  ≤

Example 1 :

Solve 23x < 100 when

(i) x is a natural number,  (ii) x is an integer.

Solution :

In order to satisfy, let us apply some random values of x.

The set of values for which the above inequality satisfy is the solution.

23x < 100 

x  =  5

23(5) < 100

115 < 100

Does not satisfy

(i) x is a natural number

Hence the required solution is

{1, 2, 3, 4} (natural number starts with 1).

(ii) x is an integer

{-∞, ...........0, 1, 2, 3, 4}

Example 2 :

Solve −2x ≥ 9 when (i) x is a real number, (ii) x is an integer, (iii) x is a natural number.

Solution :

First, let us solve for x

−2x ≥ 9

Divide both sides by -2

x ≤ -9/2

(i) x is a real number

The above inequality satisfies for every negative values of x upto -9/2.

Hence the required solution is (-∞, -9/2]

(ii) x is an integer

Since the value of x must be integer, we could not choose a rational number for x.

Hence the required solution is -∞, .............,-7, -6, -5 

(iii) x is a natural number

Natural number starts with 1, so we have to choose only positive numbers.

So, there is no solution.

Example 3 :

Solve for x

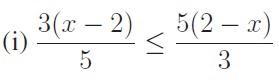
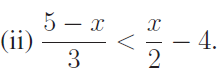
Solution :

(i)    9 (x - 2) ≤ 25 (2 - x)

9x - 18 ≤ 50 - 25x

Add both sides by 25x.

9x + 25x - 18 ≤ 50

34x - 18 ≤ 50

Add both sides by 18

34x ≤ 50 + 18

34x ≤ 68

Divide both sides by 34

x ≤ 68/34

x ≤ 2

So, the required solution is (-∞, 2].

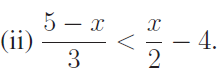
Solution :

(5 - x)/3 < (x - 8)/2

2(5 - x) < 3(x - 8)

10 - 2x < 3x - 24

Subtract both sides by 3x

10 - 5x < -24

Subtract both sides by 10

-5x < -24 - 10

-5x < -34

x > 34/5

So, the required solution is [34/5, ∞).

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.