SOLVING LINEAR INEQUALITIES IN ONE VARIABLE

Problem 1 :

4 + 6x ≤ x + 6x

Solution :

Simplify both sides of the inequality.

6x + 4 ≤ 7x

Subtract 7x from both sides.

6x + 4 - 7x ≤ 7x - 7x

-x + 4 ≤ 0

Subtract 4 from both sides.

-x + 4 - 4 ≤ 0 - 4

-x ≤ -4

Since we divide both sides by -1, change inequality > into <.

-x/-1 ≤ -4/-1

x ≥ 4

Problem 2 :

m + 16 > 8m + 2

Solution :

Subtract 8m from both sides.

m + 16 - 8m > 8m + 2 - 8m

-7m + 16 > 2

Subtract 16m from both sides.

-7m + 16 - 16 > 2 - 16

-7m > -14

Divide both sides by -7.

-7m/-7 > -14/-7

m < 2

Problem 3 :

2r - 5 > 2r - 5

Solution :

Subtract 2r from both sides.

2r - 5 - 2r > 2r - 5 - 2r

-5 > -5

Since, -5 and -5 are equal the condition will not exists for any value of r. So, there is no solution for x.

Problem 4 :

5x - 1 ≥ 13 - 2x

Solution :

Add 2x to both sides.

5x - 1 + 2x ≥ 13 - 2x + 2x

7x - 1 ≥ 13

Subtract 13 to both sides.

7x-1-13 ≥ 13-13

7x-14 ≥ 0

7x ≥ 14

x ≥ 2

Problem 5 :

6-4n < -1-4n

Solution :

Simplify both sides of the inequality.

-4n+6 < -4n-1

Add 4n to both sides.

-4n+6+4n < -4n-1+4n

6 < -1

Since this is a false condition, there is no solution for n.

Problem 6 :

-7n+3n > -9-7n

Solution :

Simplify both sides of the inequality.

-4n > -7n-9

Add 7n to both sides.

-4n+7n > -7n-9+7n

3n > -9

Divide both side by 3

3n/3 > -9/3

n > -3

Problem 7 :

1+2m ≥ 8+m

Solution :

Subtract –m from both sides

1+2m-m ≥ 8+m-m

1+m ≥ 8

m ≥ 8-1

m ≥ 7

Problem 8 :

p-1 > 13+3p

Solution :

Subtract 3p from both sides.

p-1-3p > 13+3p-3p

-2p-1 > 13

-2p > 13+1

-2p > 14

Since we divide by -2, change inequality > as <.

-2p/-2 > -14/2

p < -7

Problem 9 :

7b + 3b > -8 + 6b

Solution :

Subtract -6b from both sides.

7b + 3b - 6b > -8 + 6b - 6b

4b > -8

Divide by 4 on both sides.

b > -2

Problem 10 :

2b - 7 ≥ -14 + 2b

Solution :

Subtract -2b from both sides.

2b - 7 - 2b ≥ -14 + 2b - 2b

-7 ≥ -14

So, there are all real numbers for b.

Problem 11 :

-3k - 2 ≥ -k + 10

Solution :

Add k from both sides.

-3k - 2 + k ≥ -k + 10 + k

-2k - 2 ≥ 10

-2k ≥ 10 + 2

-2k ≥ 12

Since we divide by -2, change inequality ≥ into ≤ .

-2k/-2 ≥ 12/-2

k ≤ -6

Problem 12 :

-8x - 3 > -3 - 8x

Solution :

Add 8x from both sides.

-8x - 3 + 8x > -3 - 8x + 8x

-3 > -3

Since, -3 and -3 are equal the condition will not exists for any value of x. So, there is no solution for x.

Problem 13 :

7 + 6x ≥ 7x + 6x

Solution :

Simplify both sides of the inequality.

7 + 6x ≥ 13x

Subtract 13x to both sides.

7 + 6x - 13x ≥ 13x - 13x

7 - 7x ≥ 0

Subtract -7 to both sides.

7 - 7x - 7 ≥ 0 - 7

-7x ≥ -7

Since we divide by -7, change inequality ≥ into ≤ .

-7x/-7 ≥ -7/-7

x ≤ 1

Problem 14 :

-15 + 8x > 8x - 3x

Solution :

Simplify both sides of the inequality.

-15 + 8x > 5x

Subtract 5x from both sides.

-15 + 8x - 5x > 5x - 5x

-15 + 3x > 0

3x > 15

x > 5 

Problem 15 :

Lauren goes shopping and has $50 to spend. She bought a T-shirt and 3 pairs of leggings. The T-shirt cost $23. Each pair of leggings cost $x

(a) Form an inequality in terms of x.

(b) Solve the inequality to ind the possible price of the leggings.

Solution :

Given that each pair of legging is x

Cost of T-shirt = $23

Number of pairs of legging = 3

a)  23 + 3x ≤ 50

b) Solve for x,

3x ≤ 50 - 23

3x ≤ 27

Dividing by 3 on both sides

x ≤ 27/3

x ≤ 9

Problem 16 :

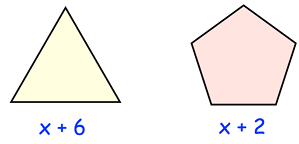
The perimeter of the regular pentagon is larger than the perimeter of the equilateral triangle.

(a) Form an inequality in terms of x

(b) Solve the inequality to find the possible range of value

Solution :

a)  Side length of equilateral triangle = x + 6

Perimeter = 3(x + 6)

Side length of regular pentagon = x + 2

Perimeter = 5(x + 2)

b)

Perimeter of regular pentagon > perimeter of equilateral triangle.

5(x + 2) > 3(x + 6)

5x + 10 > 3x + 18

5x - 3x > 18 - 10

2x > 8

x > 8/2

x > 4

So, the possible range is x > 4.

Problem 17 :

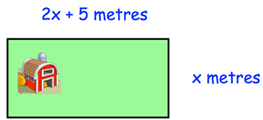
Farmer Taylor is placing a fence around his field. He has 300 metres of fencing but this is not enough.

(a) Form an inequality in terms of x.

(b) Solve the inequality to find the possible width of the ie

Solution :

Length = 2x + 5

Width = x

a) Perimter = 2 (length + width)

= 2 (2x + 5 + x)

= 2(3x + 5)

2(3x + 5) > 300

3x + 5 > 150

3x > 145

x > 145/3

x > 48.3

b)  So, the value of x should be greater than 48.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.