SOLVING LINEAR EQUATIONS IN TWO VARIABLES USING ELIMINATION METHOD

General form of linear equation in two variables is ax + by + c =  0

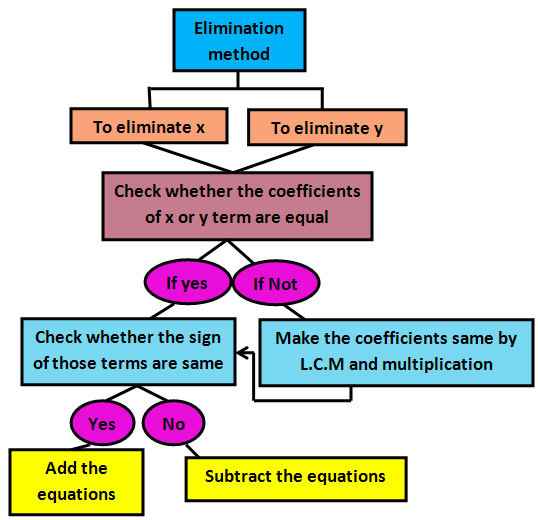
• Using the elimination method, we can  eliminate any one of the variables by combining both equations. 
• We can do elimination if and only if the coefficients are same. 
• If they are different, then we have to make the coefficients as same and then we may continue elimination.
• If the coefficients along with the signs are same, we may do elimination by subtracting both the equations.
• If the signs are different and coefficients are same, then we may do elimination by adding both the equations.
• By applying the value of variable we get from the previous step in either of the equations, we will get the value of the remaining variable.

The flow chart given below will help us to understand the procedure better.

Solve the following system of linear equations by elimination method

Question 1 :

13x + 11y  =  70 ,  11x + 13y  = 74

Solution :

13x + 11y  =  70   -------- (1)

11x + 13y  =  74 -------- (2)

By considering the given equations,

Coefficient of x in (1)  =  Coefficient of y in (2)

Coefficient of y in (1)  =  Coefficient of x in (2)

(1) + (2)

24 x + 24 y = 144

Divide the entire equation by 24, we get

x + y  =  6  ------- (3)

(1) - (2)

2x – 2y  =  -4

By dividing the entire equation by 2, we get

x – y  =  -2------- (4)

x +  y  =  6

x –  y  = -2

---------------

2 x = 4

x = 2

Substitute x = 2 in the (3)

2 + y  =  6

y  =  6 – 2

y  =  4

Hence the solution is (2, 4).

Question 2 :

65x – 33y  =  97 and 33x – 65y  =  1

Solution :

 65x – 33y  =  97  ------- (1)

 33x – 65y  =  1  ---------(2)

By considering the given equations,

Coefficient of x in (1)  =  Coefficient of y in (2)

Coefficient of y in (1)  =  Coefficient of x in (2)

(1) + (2)

98x - 98y  =  98

By dividing the entire equation by 98

 x - y  =  1  ------- (3)

(1) - (2)

  32x + 32y  =  96

By dividing the entire equation by 32, we get

x + y = 3  ------- (4)

x -  y  =  1

x + y  =  3

---------------

2 x  =  4

  x  =  2

Substitute x = 2 in (3)

2 - y  =  1

- y  =  1 – 2

y  =  1 

Hence the solution is (2, 1).

Question 3 :

A grain storage warehouse has a total of 30 bins. Some hold 20 tons of grain each, and the rest hold 15 tons each. How many of each type of bin are there if the capacity of the warehouse is 510 tons

Solution :

Let x be the number of bins hold 20 tons

Let y be the number of bins hold 15 tons

x + y = 30 -----(1)

20x + 15y = 510

Dividing by 5,

4x + 3y = 102 -----(2)

(1) ⋅ 3 - (2) ==> (3x + 3y) - (4x + 3y) = 90 - 102

-x = -12

x = 12

Applying the value of x in (1), we get

12 + y = 30

y = 30 - 12

y = 18

Number of bins contain 20 tons = 12

Number of bins contain 15 tons = 18

Question 4 :

Tickets for the homecoming dance cost $20 for a single ticket or $35 for a couple. Ticket sales totaled $2280, and 128 people attended. How many tickets of each type were sold?

Solution :

Let x be the number of single tickets

Let y the number of couple tickets

Amount collected = $2280

Total number of tickets = 128

20x + 35y = 2280 ------(1)

x + 2y = 128------(2)

From (2), x = 128 - 2y

Applying the value of y in (1), we get

20 (128 - 2y) + 35y = 2280

2560 - 40y + 35y = 2280

2560 - 5y = 2280

2560 - 2280 = 5y

5y = 280

y = 280/5

y = 56

Applying the value of y in (2), we get

x + 2(56) = 128

x + 112 = 128

x = 128 - 112

x = 16

Number of single tickets = 16

Number of couple tickets = 56/2 ==> 28

Question 5 :

Solve the system by elimination method

x + y = 72 and 0.10x + 0.25y = 15.90

Solution :

x + y = 72 -----(1)

0.10x + 0.25y = 15.90 ----(2)

Dividing equation (2) by 0.10 

1x + 2.5y = 159 -----(2)

(1) - (2)

x + y - x - 2.5y = 72 - 159

-1.5y = -87

y = 87/1.5

y = 58

Applying the value of y in (1), we get

x + 58 = 72

x = 14

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.