SOLVING LINEAR EQUATIONS IN TWO VARIABLES BY SUBSTITUTION

Solve the following pairs of linear equations by substitution.

Example 1 :

x + y = 14 and x - y = 4

Solution :

x + y = 14 ----(1)

x - y = 4 ----(2)

In (1), solve for y in terms of x.

y = 14 - x

Substitute y = 14 - x.

x - (14 - x) = 4

x - 14 + x = 4

2x - 14 = 4

Add 14 to both sides.

2x = 18

Divide both sides by 2.

x = 9

Substitute x = 9 in y = 14 - x.

y = 14 - 9

  y = 5

So, the solution is (x, y) = (9, 5).

Example 2 :

s - t = 3 and s/3 + t/2 = 6

Solution :

s - t = 3 ----(1)

s/3 + t/2 = 6 ----(2)

In (1), solve for s in terms of t.

s = 3 + t

Substitute s = 3 + t in (2).

(3 + t)/3 + t/2 = 6

Least common multiple of (3, 2) is 6. Multiply both sides of the equation by 6 to get rid of the denominators 3 and 2.

6[(3 + t)/3 + t/2] = 6(6)

6[(3 + t)/3] + 6(t/2) = 36

2(3 + t) + 3t = 36

6 + 2t + 3t = 36

6 + 5t = 36

Subtract 6 from both sides.

5t = 30

Divide both sides by 5.

t = 6

Substitute t = 6 in s = 3 + t.

s = 3 + 6

s = 9

So, solution is (s, t) = (9, 6).

Example 3 :

3x - y = 3 and 9x - 3y = 9

Solution :

3x - y = 3 ----(1)

9x - 3y = 9 ----(2)

In (1), solve for y in terms of x.

3x - y = 3

-y = -3x + 3

y = 3x - 3

Substitute y = 3x - 3 in (2).

9x - 3(3x - 3) = 9

9x - 9x + 9 = 9

9 = 9

In the last step, the variable is no more. and also the result 9 = 9 is a true statement. So, the given pair of linear equations has infinitely many solutions.

Example 4 :

Describe and correct the error in solving for one of the variables in the linear system 8x + 2y = −12 and 5x − y = 4.

Solution :

The given system of equations are

8x + 2y = -12 -----(1)

5x - y = 4  ------(2)

From (2),

-y = -5x + 4

y = 5x - 4

Solve for y correctly in the given picture above.

Applying the value of y in (1), we get

8x + 2(5x - 4) = -12

8x + 10x - 8 = -12

18x = -12 + 8

18x = - 4

x = -4/18

x = -2/9

To solve the system of equation,

• First we have to get the value of one variable in terms of other variable. 
• Then we have to apply the equation derived for one variable in terms of other variable in the other equation.

The error is after deriving for one variable, they have applied the value in the same equation. So, we get no solution. 

Example 5 :

Describe and correct the error in solving for one of the variables in the linear system 4x + 2y = 6 and 3x + y = 9.

Solution :

4x + 2y = 6 -----(1)

3x + y = 9 -----(2)

Deriving the value of y from (2)

y = 9 - 3x

Applying the value of y in (1), we get

4x + 2(9 - 3x) = 6

4x + 18 - 6x = 6

-2x + 18 = 6

-2x = 6 - 18

-2x = -12

x = 6

Applying the value of x in (2) as shown.

3(6) + y = 9

18 + y = 9

y = 9 - 18

y = -9

The error is instead of applying the value of x as 6, they have applied the value of y as 6.

Example 6 :

An investor owns shares of Stock A and Stock B. The investor owns a total of 200 shares with a total value of $4000. How many shares of each stock does the investor own?

Solution :

Let x be the number of shares in stock A and y be the number of shares in stock B.

Total number of shares = 200

x + y = 200 -----(1)

Value of the shares = $4000

9.50x + 27y = 400 ------(2)

From (1), we get

y = 200 - x

Applying the value of y in (2), we get

9.50x + 27(200 - x) = 4000

9.50x + 5400 - 27x = 4000

-17.5 x + 5400 = 4000

-17.5x = 4000 - 5400

x = 1400/17.5

x = 80

Applying the value of x in y = 200 - x

y = 200 - 80

y = 120

Number of shares in stock A is 80 and number of shares in stock B is 120.

Example 7 :

(a) write an equation that represents the sum of the angle measures of the triangle and (b) use your equation and the equation shown to fi nd the values of x and y

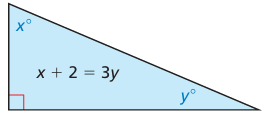
Solution :

x + 2 = 3y

x = 3y - 2 -----(1)

x + y + 90 = 180

x + y = 180 - 90

x + y = 90 -----(2)

Applying the value of x in (2), we get

3y - 2 + y = 90

4y = 90 + 2

y = 92/4

y = 23

Applying the value of y in (1)

x = 3(23) - 2

x = 69 - 2

x = 67

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.