SOLVING SYSTEM OF EQUATIONS BY GRAPHING

Solve each system by graphing.

Example 1 :

x + y = 7; x - y = 3

Solution :

x + y = 7 -----(1) 

x − y = 3 -----(2)

From (1),

y  =  7 - x

Substitute some random values for x and solve for y. 

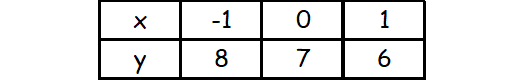
The points on the first line are

(-1, 8), (0, 7), (1, 6)

From (2),

y  =  x - 3

Substitute some random values for x and solve for y. 

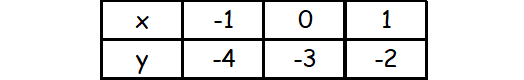
The points on the second line are

(-1, -4), (0, -3), (1, -2)

Plot the points from the above tables and sketch the graph. 

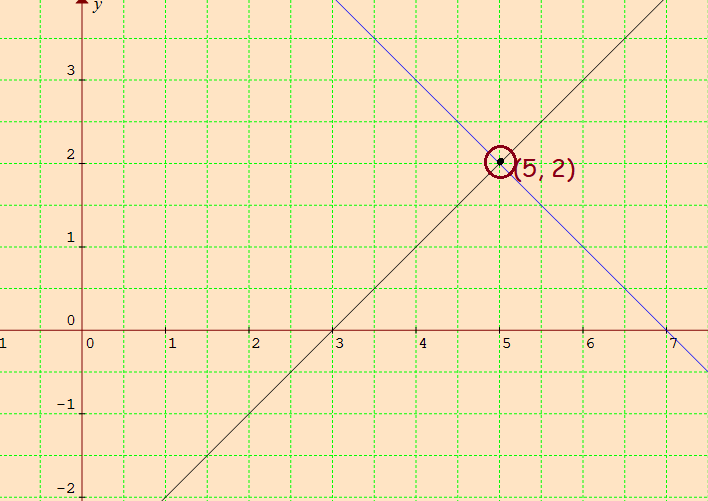
The point of intersection of the two lines is the solution.

So, the solution is (x, y) = (5, 2).

Example 2 :

3x + 2y = 4; 9x + 6y - 12 = 0

Solution :

3x + 2y = 4 -----(1)

9x + 6y = 12 -----(2)

From (1),

2y  =  -3x + 4

y  =  (-3x + 4)/2

y  =  -3x/2 + 4/2

y  =  -3x/2 + 2

From (2),

6y  =  -9x + 12

y  =  (-9x + 12)/6

y  =  -9x/6 + 12/6

y  =  -3x/2 + 2

Because both the lines are same, it has infinitely many solution.

Example 3 :

(x/2) + (y/4) = 1

(x/2) + (y/4) = 2

Solution :

Because the coefficients of x and y are same, they are parallel lines and they never intersect. So, there is no solution. 

Example 4 :

x - y = 0; y + 3 = 0

Solution :

x - y = 0 -----(1)

y + 3 = 0 -----(2)

From (1),

-y  =  -x

y  =  x

Substitute some random values for x and solve for y. 

The points on the first line are

(-1, -1), (0, 0), (1, 1)

From (2), 

y  =  -3

Plot the points from the above table and sketch the graph. 

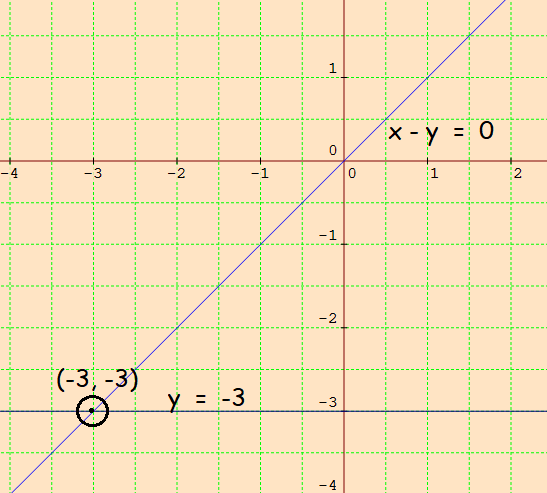
Two lines intersect at (-3, -3). 

So, the solution is (x, y) = (-3, -3).

Example 5 :

  y = 2x + 1; y + 3x - 6 = 0

Solution :

y = 2x + 1 -----(1)

y + 3x = 6 -----(2)

From (1),

y  =  2x + 1

Substitute some random values for x and solve for y. 

The point on the first line are

(-1, -1) (0, 1), (1, 3)

From (2),

y + 3x  =  6

 y  =  -3x + 6

Substitute some random values for x and solve for y. 

The point on the first line are

(-1, 9) (0, 6), (1, 3)

Plot the points from the above tables and sketch the graph. 

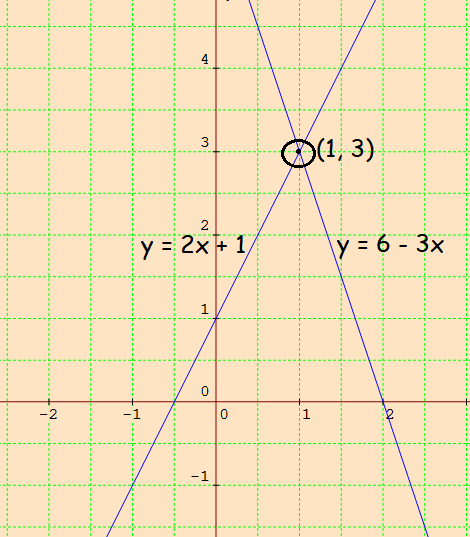
Two lines intersect at (1, 3). 

So, the solution is (x, y) = (1, 3).

Example 6 :

x = -3 ; y = 3

Solution :

Sketch the graph of x = -3 and y = 3.  

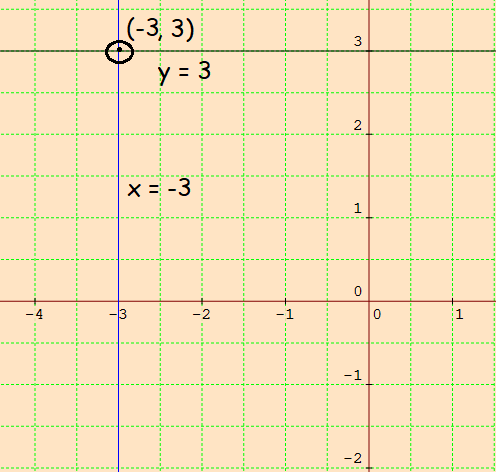
The two lines intersect at (-3, 3). 

So, the solution is (-3, 3). 

Example 7 :

Two cars are 100 miles apart. If they drive towards each other they will meet in 1 hour. If they drive in the same direction they will meet in 2 hours. Find their speed by using graphical method.

Solution :

Let x and y be the speeds of the cars in miles per hour. 

Given : Cars are 100 miles apart. If they drive towards each other, they will meet in 1 hour.

x + y  =  100

y  =  -x + 100 -----(1)

Substitute some random values for x and solve for y. 

Given :  If they drive in the same direction they will meet in 2 hours. 

Distance  =  Speed x Time

Distance covered by the cars in two hours :

2x miles, 2y miles

They meet after 2 hours.

2x  =  2y + 100

x  =  y + 50

y  =  x - 50 -----(2)

Substitute some random values for x and solve for y. 

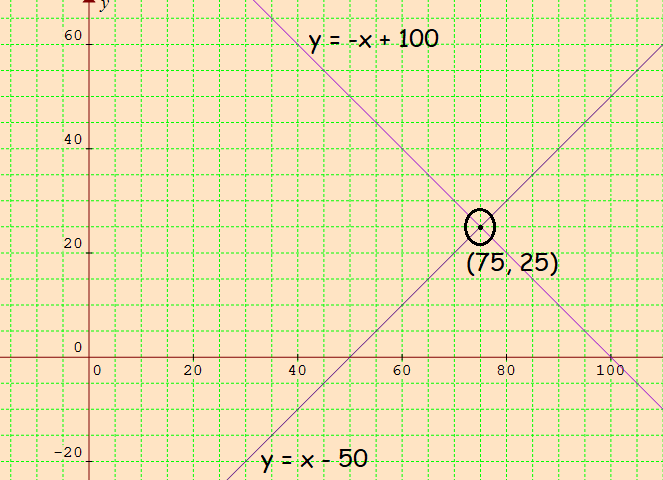
The two lines intersect at (75. 25). 

(x, y)  =  (75, 25)

Speeds of the cars are 75 miles per hour and 25 miles per hour. 

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.