SOLVING INEQUALITIES INVOLVING RATIONAL FUNCTIONS

The forms of inequalities involving rational functions :

(i)  (ax + b) / (cx + d)  >  0

(ii)  (ax + b) / (cx + d)  <  0

(iii)  (ax + b) / (cx + d)  ≥  0

(iv)  (ax + b) / (cx + d)  ≤  0

If the given question is in one of the above forms, we may follow the steps given below to solve the inequality.

If we have any numerical value other than zero on the right side, we have to make it zero using addition or subtraction. 

Step 1 :

Make sign of coefficient of x as positive, if they are not.

Step 2 :

Equate the numerator and denominator to zero and find the values of x. These values are known as critical number.

Step 3 :

Draw the number line and plot critical numbers.

Step 4 :

These critical numbers will divide the number line into three regions.

Step 5 :

In the right most  region the expression on L.H.S of the equation obtained in the step 4 will be positive and other regions will be alternatively negative and positive in other regions.

Step 6 :

• If the given question has the inequalities < or ≤, we have to choose the intervals in the negative region.
• If the given question has the inequalities > or ≥, we have to choose the interval in the positive region.

Example 1 :

Solve the following linear inequations

(2x + 4)/(x - 1)  ≥  5

Solution :

(2x + 4)/(x - 1)  ≥  5

By subtracting 5 on both sides, we get

[(2x + 4)/(x - 1)] - 5  ≥  5 - 5

[(2x + 4) - 5(x - 1)]/(x - 1)  ≥  0

(2x + 4 - 5x + 5)/(x - 1)  ≥  0

(-3x + 9)/(x - 1)  ≥  0

-3(x - 3)/(x - 1) ≥  0

Multiply by -3 throughout the equation, we get

(x - 3)/(x - 1) ≤  0

By equating the numerator and denominator to zero, we get

x - 3   = 0 ,   x - 1  =  0

x  =  3 and x  =  1

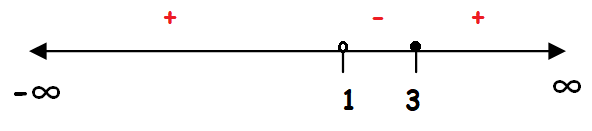
The critical number is dividing the number line into three regions.

We have used unfilled circle for 1 and filled circle for 3.Because if the numerator will become zero, the entire function will become zero. 

We should not make the denominator as zero.

Since we have greater than sign (≤) in the last step, we have to choose only negative region.

So, the solution set of given equation is (1, 3]

Example 2 :

Solve the following linear inequality

(x - 2)/(x + 5) > 2

Solution :

(x - 2)/(x + 5) > 2

Subtract by 2 throughout the equation

[(x - 2)/(x + 5)] - 2 > 2 - 2

By taking L.C.M we get,

[(x - 2) - 2(x + 5)}/(x + 5) > 0

(x - 2 - 2x - 10)/(x + 5) > 0

-x - 12/(x + 5) > 0

- (x + 12)/(x + 5) > 0

In order to make the coefficient x as positive, we have to multiply by -1 through out the equation

(x + 12)/(x + 5) < 0

So the > has being converted into <.

Equate the numerator and denominator to zero, we get

x + 12 = 0    x + 5 = 0

x = -12 and x = -5 (Critical numbers)

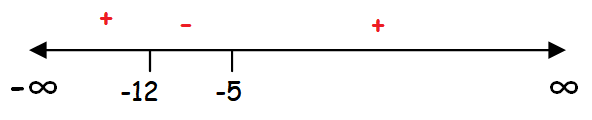
The critical number is dividing the number line into three regions.

Since we have greater than sign (<) in the last step, we have to choose only negative regions.

So, the solution set of given equation is (-12, -5).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.